Краткие теоретические сведения. В электрических цепях переменного тока имеются цепи с параллельным соединением

В электрических цепях переменного тока имеются цепи с параллельным соединением потребителей электроэнергии, при котором все потребители находятся под одним и тем же напряжением. При этом на ток в цепи каждого из потребителей не влияет на их количество. Значение тока в каждом из них определяется только значениями соответствующих сопротивлений и значением подводимого напряжения.

Примером электрической цепи переменного тока с параллельным соединением сопротивлений может служить цепь, представленная на рисунке 3.2

Рисунок 3.2. Параллельное соединение двух приемников

Рассматривая отдельные параллельные ветви представленной цепи как независимые электрические цепи, для каждой из них можно построить векторную диаграмму.

Токи приемников можно определить по закону Ома:

, ,

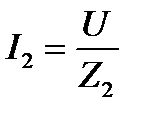где , .

Зная величину токов I₁, I₂ и разность фаз φ₁, φ₂ построим векторную диаграмму. За основной вектор примем вектор . Его отложим по горизонтальной оси. Ток индуктивного характера, он отстает от вектора напряжения на угол φ₁, ток — емкостного характера, опережает на угол φ₂. В общем случае, когда приемник включает в себя все три элемента R, L и С,ток будет отставать по фазе от напряжения или опережать его; в зависимости от того, какое сопротивление преобладает в ветви - индуктивное или емкостное.

Ток в неразветвленной части согласно первому закону Кирхгофа . Складывая векторы и , найдем общий ток и разность фаз тока и напряжения - угол φ. Численно значение тока I равно длине вектора в принятом на диаграмме масштабе для токов.

Так можно рассчитать разветвленную цепь с двумя приемниками. Для цепи с большим числом параллельных ветвей векторная диаграмма становится громоздкой.

Вектор тока можно рассматривать состоящим из суммы двух векторов и . Вектор , совпадающий по фазе с напряжением, назы­вают активной составляющей тока . Второй вектор , отстающий от на­пряжения на угол π/2, называют реактивной составляющей тока .

. Активная и реактивная составляющие тока и треугольник токов

Ток , его активная и реактивная составляющие образуют прямоугольный треугольник - треугольник токов. Из треугольника токов

I_1a = I₁ cos φ₁; I_1р = I₁ sin φ₁; .

Ток любой ветви можно рассматривать как геометрическую сумму его активной и реактивной составляющих:

.

Рассмотрим разложение токов и на активные и реактивные составляющие (Рисунок). Активная составляющая общего тока I_a равна сумме активных составляющих токов I_1a и I_2a. Реактивная составляющая общего тока I_р равна разности реактивных составляющих токов I_1р и I_2р. Ток в неразветвленной части схемы из треугольника токов . Относительно напряжения он сдвинут на угол .

 

Векторная диаграмма при разложении токов на активные и реактивные составляющие.

Проводимости. Треугольник проводимостей.

Разделив каждую сторону треугольника токов на напряжение, получим подобный ему треугольник – треугольник проводимостей.

Рисунок Треугольник токов и треугольник проводимостей.

Величина обратная полному сопротивлению, называется полной проводимостью.

Активная проводимость 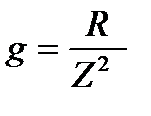. Если ветвь содержит только активное сопротивление R и, следовательно, полное сопротивление ветви (здесь Х = 0), то активная проводимость g имеет такой же вид, как и в цепи постоянного тока: .

Реактивная проводимость . Реактивная проводимость ветви может быть индуктивной или емкостной и соответственно положительной или отрицательной. В общем случае, когда приемник (ветвь) содержит оба параметра L и С, реактивное сопротивление ветви X=X_l - X_c. Если X_l > X_c, или емкость совсем отсутствует (X_c =0), то Х>0 и реактивная проводимость - индуктивная; она имеет положительное значение: 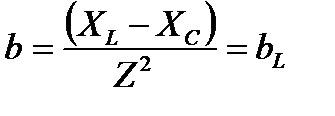. Если же X_l < X_cили индуктивность отсутствует (X_l = 0), то Х<0, и реактивная проводимость - емкостная и имеет отрицательное значение: .

Если ветвь содержит параметр L (R=0), то полное сопротивление . Активная проводимость g=0; реактивная проводимость .

Если ветвь содержит параметр С (R=0), то полное сопротивление . Активная проводимость g=0; реактивная проводимость .

Активная g, реактивная bи полная Y проводимости связаны между с формулами прямоугольного треугольника:

; ; ; .

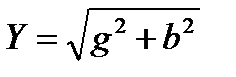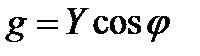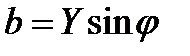В цепях переменного тока с параллельным соединением различных по характеру сопротивлений (рисунок 3.1.) может возникнуть резонанс токов. Резонансом токов называется явление, при котором в электрической цепи с параллельно соединенными R, L, C, ток в неразветвленной части цепи, совпадает по фазе с напряжением. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление. Резонанс токов (явление резонанса на участке электрической цепи, содержащей параллельно соединенные индуктивный и емкостный элементы) — особое состояние цепи переменного тока при параллельном соединении сопротивлений, при котором реактивная индуктивная проводимость оказывается равной реактивной емкостной проводимости этой цепи, т. е. при условии, что B_L=B_C.

Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Полная проводимость рассматриваемой цепи

Резонанс токов можно получить путем изменения частоты источника питания или изменением индуктивности и емкости при по­стоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении ука­занных параметров.

Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяют в радиоэлектронике в качестве колебательных контуров, в которых резонанс токов достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.

Резонанс токов характеризуется следующими явлениями.

1. При резонансе токов полная проводимость всей электриче­ской цепи приобретает минимальное значение и становится равной активной ее составляющей (B_L=B_C):

.

2.Минимальное значение проводимости обусловливает и минимальное значение тока цепи:

.

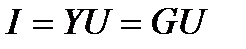3. Емкостный ток I_Cи индуктивная составляющая I_Lтока ка­тушки оказываются при этом равными по величине, а активная
составляющая тока катушки I_Rстановится равной току I,потреб­ляемому из сети. При этом реактивные составляющие тока I_Lи I_C(в зависимо­сти от значения реактивных проводимостей) могут приобретать теоретически весьма большие значения и намного превышать ток I, потребляемый электрической цепью из сети.

4. Реактивная составляющая полной мощности, потребляе­мой цепью, при B_L=B_C оказывается равной нулю:

.

При этом индуктивная и емкостная составляющие реактив­ной мощности также могут приобретать весьма большие значе­ния, оставаясь равными» друг другу.

5. Полная мощность цепи при резонансе равна ее активной
составляющей

.

6. Коэффициент мощности всей цепи при резонансе:

.

Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности (cosφ), так как он имеет большое технико-экономическое значение. Повышение коэффициента мощности обеспечивается подключением конденсаторов (или других источников реактивной емкостной мощности) параллельно потребителям электрической энергии, которые вследствие наличия свойственной им индуктивности имеют низкий коэффициент мощности.

Дата добавления: 2015-08-17