Исследование трёхфазных цепей, соединенных звездой

1. Цель работы:

1.1. Исследование режимов работы симметричного и несимметричного потребителей электрической энергии в трехфазных электрических цепях, соединенных звездой.

1.2. Определение основных соотношений между фазными и линейными значениями токов и напряжений при симметричной нагрузке и включении потребителей звездой.

2. Подготовка к работе:

2.1. Ознакомится с описанием работы, указанной литературой и краткими сведениями из теории.

2.2. Начертить схему трехфазной симметричной цепи, соединенную звездой с нейтральным проводом. При U_A=100 В вычислить фазные (линейные) токи I_A, I_B, I_C и ток в нейтральном проводе I_N для двух режимов:

а) симметричный Z_A=Z_B=Z_C=20 Ом,

б) несимметричный Z_A=Z_B=20 Ом, Z_C=40 Ом.

Записать результаты расчета в таблицу 4.1.

Таблица 4.1.

Результаты расчетов

Режим цепи

Фазные ЭДС

Линейные напряжения

Фазные напряжения

Фазные (линейные) токи

ЕА

ЕВ

ЕС

UAB

UBC

UCA

UA

UB

UC

IA

IB

IC

IN

В

В

В

В

В

В

В

В

В

A

A

A

A

симметр

несиметр

Построить векторную диаграмму токов и напряжений цепи для симметричного и не симметричного режимов.

2.3. Начертить схемы и таблицы экспериментальной части работы.

3. Краткие сведения из теории.

В современных условиях электрическая энергия вырабатывается преимущественно источниками энергии с трёхфазной системой напряжений. Такие источники широко применяют в технике. Объясняется это тем, что трехфазная система переменного тока является наиболее экономичной. В качестве трехфазных источников напряжений на электрических станциях используют трехфазные синхронные генераторы, на статоре которых размещаются три фазные обмотки (фазы), смещенные в пространстве относительно друг друга на угол 120⁰. При вращении ротора, выполненного в виде электромагнита постоянного тока, в обмотках генератора будут индуцироваться переменные ЭДС, сдвинутые относительно друг друга по фазе также на 120⁰ (2π/3): е_A=E_Аm×sin t; е_В=E_Вm×sin (ω t- 2π/3); е_С=E_Сm×sin (ω t+ 2π/3),

где E_Аm= E_Вm= E_Сm – значения ЭДС соответственно фаз А, В, С.

Рис. Т. 13. Трехфазная система ЭДС

Таким образом, под трехфазной системой понимается совокупность однофазных цепей, в которых действуют три синусоидальные ЭДС (напряжения) одной и той же частоты, сдвинутые относительно друг друга по фазе на угол 2π/3, создаваемые общим источником электрической энергии.

Под действием трехфазной системы ЭДС на зажимах трех­фазного потребителя создается трехфазная симметричная система напряжений, сдвинутых по фазе на угол 120°, т. е. на угол 2π/3, и имеющих одинаковые амплитудные и действующие значения U_АВ = U_ВС = U_СА.

В трехфазной системе потребители электроэнергии соединя­ются звездой или треугольником. На рис. 6.2 приведена схема раздельного подключения трех фаз источника энергии к трем фазам приемника.

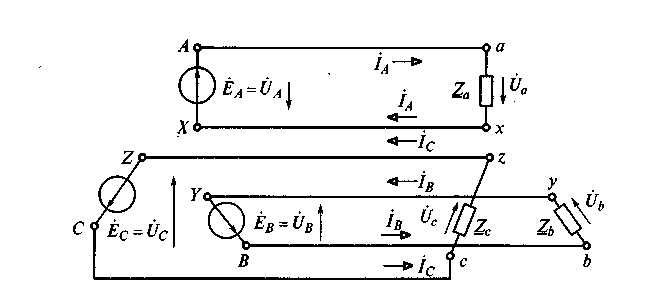
Положительные направления фазных ЭДС определяют «начало» (А, В, С) и «концы» (X, Y, Z) фазных обмоток источника. Одноименными строчными буквами обозначаются выводы фаз приемника.

Соединение фаз источника и приемника звездой (условное обозначение X) приведено на рис. 6.3, где выводы источника X, Y, Z и выводы приемника х, у, z объединены в узел N и узел п соответственно. Эти узлы называются нейтральными точками источника и приемника, а провод, соединяющий их, - нейтральным проводом. Остальные три провода, соединяющие одноименные выводы источника и приемника, называются линейными.

При расчете трехфазных цепей пользуются понятиями фазных и линейных токов и напряжений.

Фазными токами и напряжениями называются токи в фазах ис­точника и приемника и напряжения между выводами фаз.

Линейными токами и напряжениями называются токи в линей­ных проводах и напряжения между ними.

Для обозначения фазных величин источника и линейных вели­чин будем пользоваться прописными буквами латинского алфавита А, В, С, для обозначения фазных величин приемника — строчными а, Ь, с

Выводы обмоток генераторов, трансформаторов обозначаются:

Различают две схемы соединения в звезду, а именно, схема соединения в звезду с нулевым проводом или четырехпроводная и схема соединения в звезду без нулевого провода или трехпроводная. Если нейтральная точка источника N соединена с нейтральной точкой приемника n, то получаем четырехпроводную схему звезды, если нет провода, соединяющего точки N-n, то получаем трехпроводную звезду.

Выбор схем соединения источника и приемника зависит от вида нагрузки. Если линия электропередачи питает только симметричные трехфазные потребител Z_A=Z_B=Z_C (трехфазные электродвигатели, трансформаторы, электрокалориферы и др.), то принимается трехпроводная схема звезды, если наряду с симметричными потребителями существуют несимметричные потребители Z_A¹Z_B¹Z_C как правило для работы потребителей необходимо принять четырехпроводную схему звезды.

Токи, протекающие через обмотки источников электрической энергии и через сопротивление нагрузок называют фазными токами, а токи, протекающие по линейным проводам – линейными токами. Соотношение между величинами линейных и фазных напряжений в трех – фазной системе при присоединении потребителя в "звезду" имеет вид:

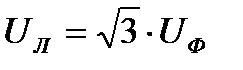
Величины линейных токов определяют из выражений:

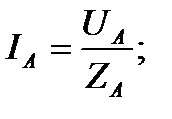
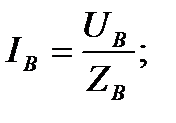
Ток в нулевом проводе I_N равен геометрической векторной сумме линейных токов:

I_N=I_A+I_B+I_C.

Так как при схеме звезда линейный провод соединяется последовательно с фазой нагрузки, то линейный ток I_Л равен фазному I_Ф.

При симметричном режиме нагрузки сумма фазных токов цепи, образующих симметричную систему векторов, равна нулю, и в нейтральном проводе тока не будет, т.к.: I_N=I_A+I_B+I_C=0. Поэтому в цепях с симметричной нагрузкой (например, трехфазный электродвигатель) для обеспечения нормальной работы нулевой провод не нужен, однако он необходим для обеспечения необходимого уровня электробезопасности.

Мощность трехфазной цепи

В любом режиме активная мощность трехфазной цепи может быть определена, как сумма активных мощностей фаз:

P_S=P_A+P_B+P_C,

где: P_A, P_B, P_C – активные мощности фаз, определяемые по формулам:

P_A=U_AФ×I_AФ×cosj_A; P_B=U_BФ×I_BФ×cosj_B; P_C=U_CФ×I_CФ×cosj_С;

Аналогично определяется и реактивная мощность трехфазной цепи, так для схемы звезда:

Q=Q_A+Q_B+Q_C,

где Q_A=U_AФ×I_AФ×sinj_A - реактивная мощность фазы А, соответственно для В, и С: Q_B=U_BФ×I_BФ×sinj_B; Q_C=U_CФ×I_CФ×sinj_С;

Полная мощность трехфазной цепи:

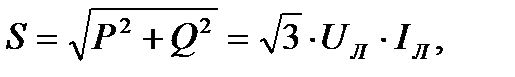ВА

Если режим цепи симметричный, то активные (и реактивные) мощности фаз равны. Тогда, например, активная мощность равна:

.

4. Экспериментальная часть.

4.1. Собрать цепь по схеме рисунок 4.1. Цепь состоит из трех амперметров, включенных в каждую из фаз, амперметра включенного в нулевой провод и вольтметра.

4.2. Установить симметричный режим и измерить фазные и линейные напряжения источника, фазные напряжения и токи на нагрузке и записать в таблицу 4.2.

Таблица 4.2.

Результаты измерений и вычислений

Режим цепи

Измерить

Вычислить

UФ

UЛ

Ua

Ub

Uc

Ia

Ib

Ic

IN

PA

PB

PC

P

В

В

В

В

В

А

А

А

А

Вт

Вт

Вт

Вт

симметр

несимметр

Рисунок 4.1. Схема трёхфазной цепи с активной нагрузкой, соединённой звездой.

4.3. Установить в цепи (рисунок 4.2) несимметричный режим. Повторить измерения п.4.2. Результаты записать в таблицу 4.2.

4.4. По данным измерений вычислить активную мощность каждой фазы и всей цепи для симметричного и несимметричного режимов. Записать результаты расчетов в таблицу 4.2.

4.5. Сравнить данные обоих режимов и сделать вывод о роли нейтрального провода.

4. Содержание отчета

После выполнения лабораторной работы студент должен обладать следующими компетенциями:

Студент должен ЗНАТЬ	Студент должен УМЕТЬ
1. Энергетические соотношения в трехфазных цепях. 2. Режимы работы трехфазных электрических цепей.	1. Соединять фазы источника и потребителя «звездой». 2. Подключать однофазных потребителей к трехфазному источнику. 3. Измерять активную мощность

5.1. Схему и таблицу, ее расчет согласно п. 2.2.

5.2. Технические характеристики, используемых в работе приборов, схемы экспериментальной части.

5.3. Таблицу экспериментальных значений и расчетные выражения согласно п.п. 4.1-4.5.

5.4. Выводы по работе.

Контрольные вопросы

1. Что представляет собой трехфазный генератор?

2. Запишите мгновенные значения трехфазной системы эдс, приняв начальную фазу эдс равной нулю.

3. Что называется симметричным режимом трехфазной цепи?

4. Можно ли назвать симметричной нагрузкой трехфазный асинхронный двигатель?

5. Что называется фазным напряжением?

6. В каком соотношении находятся фазные и линейные напряжения при симметричном режиме трехфазной цепи, соединенной звездой.

7. Как графически определить ток в нейтральном проводе, если известны фазные токи?

8. Чему равна сумма мгновенных значений фазных токов при симметричном режиме трехфазной цепи, соединенных звездой?

9. Какова роль нейтрального провода трехфазной цепи?

10. Как вычислить активную мощность трехфазной цепи в симметричном режиме?

1. Тестовые задания к лабораторной работе №4

1. При вращении рамок против часовой стрелки в них индуцируются ЭДС. Какие ЭДС индуцируются при вращении рамок по часовой стрелке?

а) Те же самые
б) Знаки начальных фаз изменятся на противоположные
в) Направления векторов ЭДС в рамках изменятся на противоположные

2. Изменится ли действующее значение трехфазной ЭДС при изменении направления вращений рамок?

а) Не изменится
б) Изменится

3. Какие характеристики ЭДС изменятся, если при прочих равных ус­ловиях увеличить частоту вращения рамок?

а) Частота и начальные фазы

б) Частота и амплитуды

в) Амплитуды и начальные фазы.

4. Сколько соединительных проводов подводят к генератору, обмотки которого образуют звезду?

а) 6

б) 3 или 4

в) 3

г) 4.

5. Укажите правильное определение фазы

а) Фазой называют аргумент синуса

б) Фазой называют часть многофазной цепи

в) Оба определения правильны.

6. Чему равно действующее значение векторной суммы фазных то­ков?

а) Сумме действующих значений фазных токов

б) Меньше суммы действующих значений фазных токов и только в предельном случае равно ей

в) Всегда меньше суммы действующих значений фазных токов.

7. Чему равен ток в нулевом проводе при симметричной трехфазной системе токов?

а) Нулю

б) Значению, меньшему суммы действующих значений фазных токов.

8. Всегда ли векторная сумма токов фаз равняется нулю при отсутствии нулевого провода?

а) Всегда

б) Не всегда

9. Может ли ток в нулевом проводе четырехпроводной цепи быть равен нулю?

а) Может

б) Не может

в) Всегда равен нулю.

10. Какой из токов в схеме, линейный, какой — фазный?

а) Оба тока линейные
б) Оба тока фазные
в) Ток I1 - линейный, ток I2 - фазный
г) Ток I2- линейный, ток I1 - фазный

11. Между различными точками схемы включены вольтметры. Какой из них показывает линейное напряжение, какой - фазное?

а) Напряжение UAО -линейное напряжение UB0 - фазное
б) Напряжение UAB— линейное, напряжение UBC - фазное
в) Напряжение UCA — линейное напряжение UCO — фазное

12. Чему равен вектор U_AC,если U_CА = U_C - U_A?

а) U_AC = -U_C - U_A

б) U_AC = U_A - U_C

в) U_AC = U_C + U_A

13. Укажите причину того, что полярная и топографическая векторные диаграммы трехфазной цепи удовлетворяют одной и той же системе векторных уравнений

а) Уравнения имеют векторную форму

б) Уравнения написаны для симметричной нагрузки

в) Векторы можно переносить параллельно их начальному положению.

14. Симметричная нагрузка соединена звездой. Линейное напряжение380 В. Определить фазное напряжение

а) 380 В

б) 250 В

в) 220 В

г) 127 В.

15. Может ли геометрическая сумма линейных токов быть отличной от нуля при отсутствии нулевого провода?

а) Может

б) Не может.

16. Будут ли меняться линейные токи при обрыве нулевого провода в случае симметричной нагрузки?

а) Будут;

б) Не будут

17. Будут ли меняться линейные токи при обрыве нулевого провода в случае несимметричной нагрузки?

а) Будут;

б) Не будут.

18. За счет чего могут измениться линейные токи при постоянной ЭДС генератора и неизменных сопротивлениях нагрузки?

а) Изменения линейных напряжений

б) Изменения фазных напряжений

в) Изменения фазных и линейных напряжений.

19. Чему равна разность потенциалов точек О и О^’при наличии нулевого провода с активным сопротивлением R₀?

а) 0

б) I₀R₀

в) U_Л.

20. Может ли нулевой провод, обладающий большим активным сопротивлением, обеспечить симметрию фазных напряжений при несимметричной нагрузке?

а) Может

б) Не может

Лабораторная работа №5

Исследование трёхфазных цепей,

Дата добавления: 2015-08-17