Краткие сведения из теории. Электрическая энергия производится, распределяется и потребляется главным образом в

Электрическая энергия производится, распределяется и потребляется главным образом в виде переменного тока. Широкое распространение переменного тока объясняется тем, что переменный ток высокого напряжения легко преобразовывать в переменный ток низкого напряжения и обратно.

Переменный ток – это ток определенной формы, периодически изменяющийся во времени. Из всех возможных форм периодических токов наибольшее распространение получили синусоидальные токи. Если кривая изменения периодического тока описывается синусоидой или косинусоидой, то такой ток называют синусоидальным. Такие токи позволяют наиболее экономично производить, предавать и распределять электрическую энергию.

Синусоидальные функции могут быть представлены тригонометрической формой записи, которая в общем виде представляется выражением , где

· мгновенное значение а - значение тока в рассматриваемый момент времени;

· амплитудное значение А_m - наибольшее значение синусоидальной величины;

В электротехнике кроме мгновенных и максимальных значений переменных синусоидальных величин используются действующие значения.

Действующим значением переменного тока называется такой постоянный ток, который на одинаковом сопротивлении R за время, равное одному периоду, выделяет такое же количество тепла, что и данный переменный ток за то же время. Действующее значение синусоидального тока, напряжения, э.д.с. меньше амплитудных в 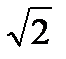раз:

где I_m, U_m, E_m – амплитудные значения силы тока, напряжения, ЭДС.

Приборы (амперметры, вольтметры), используемые в лаборатории, показывают действующие значения.

· фаза или фазовый угол - аргумент синусоидальной функции , (град, рад);

· начальная фаза (угол) φ_о - значение фазы в начальный момент времени t=0;

· угловая частота тока ω - скорость изменения фазового угла 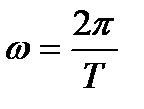или ,

где период Т - промежуток времени, через который начинается повторение периодического тока (переменная величина принимает все возможные значения),

частота f - величина, обратная периоду (число периодов в единицу времени);

Для синусоидального тока промышленной частоты: f=50 Гц, ω=314 с^-1, ;

Расчет линейных электрических цепей синусоидального тока

Любое электротехническое устройство можно представить в виде соединенных между собой определенным образом идеализированных элементов: резисторов, катушек индуктивности и конденсаторов. Все перечисленные электротехнические устройства обладают электрическим активным сопротивлением R, индуктивностью L и емкостью С.

При соединении резистора к источнику переменного синусоидального тока через него начинает протекать синусоидальный ток, совпадающий по фазе с напряжением. При включении в цепь переменного тока идеализированной катушки индуктивности через нее проходит синусоидальный ток, вектор которого отстает от вектора напряжения на угол π/2 рад. (90°). При включении в цепь переменного тока конденсатора, через него протекает ток, опережающий напряжение на его зажимах на π /2 рад. (90°).

При расчете электрических цепей переменного тока синусоидальные функции изображают векторами. Совокупность векторов, изображающих токи и напряжения одной электрической цепи называют векторной диаграммой. Рассмотрим электрическую цепь (рисунок), состоящую из последовательно включенных активного сопротивления R, индуктивности L и емкости С, ток один и тот же на всех, участках. Принимая начальную фазу тока равной нулю, изобразим его вектором (рис. 6-3, а).

Рис. 6-2. Схема последовательного соединения элементов R, L и С.

Рассмотрим каждый участок в отдельности. На участке с активным сопротивлением R активное падение напряжения u_а совпадает по фазе с током, вектор направлен параллельно вектору тока 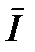. На участке с индуктивностью падение напряжения опережает ток на 90°; вектор 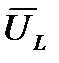направлен под углом π/2 в сторону опережения относительно вектора 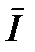. На участке с емкостью напряжение u_с отстает от тока на 90°; вектор 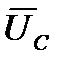направлен под углом π/2 в сторону отставания от вектора .

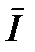Входное напряжение можно найти, составив для схемы рис. 6-2 уравнение по второму закону Кирхгофа: u= u_A+ u_L+ u_C.

Рис. 6-3. Векторы тока и напряже­ний на элементах цепи а) и вектор­ная диаграмма б).

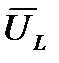Осталось сложить эти три вектора: к концу вектора пристроить вектор , а к концу вектора 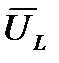- вектор 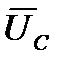(рис. 6-3, б). Соединив начало координат (точку О) с концом последнего вектора, найдем вектор . Длина вектора укажет величину вводного напряжения, а угол φ - его начальную фазу. Так как начальную фазу тока приняли равной нулю, то напряжение можно записать уравнением .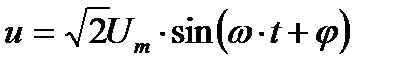

Векторы напряжений на индуктивности 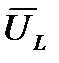и емкости 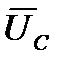направлены противоположно. Их разность U_L –U_C=U_рназывают реактивным напряжением.

Образовавшийся на векторной диаграмме (рис. 6-3, б) прямоугольный треугольник называют треугольником напряжений. Катетами треугольника являются активная U_аи реактивная U_р составляющие напряжения, а гипотенузой — вектор входного напряжения . Для треугольника напряжений справедливы все соотношения прямо­угольного треугольника, например

.

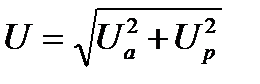U_а, U_р как проекции вектора напряжения на вектор тока равны: U_а = U cos φ, U_р = U sin φ.

Реактивная составляющая напряжения по величине равна разности индуктивного U_L=X_LI и емкостного U_C=X_CI падений напряжений:

,

где - индуктивное сопротивление, пропорциональное угловой частоте тока и индуктивности L;

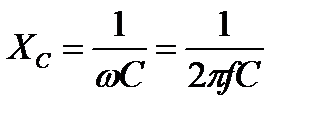- емкостное сопротивление, обратно пропорциональное угловой частоте и емкости конденсатора С;

- реактивное сопротивление.

Если стороны треугольника напряжения (рис. 6-4) разделить на ток, то получим подобный треугольник, катеты которого в определенном масштабе изображают активное R и реактивное Х=Х_L -Х_Cсопротивления. Гипотенуза треугольника получила название полного сопротивления:

.

Из треугольника сопротивлений полное сопротивление .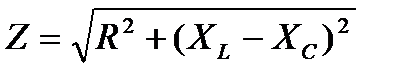

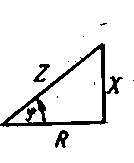
6-4Треугольник напряжение и треугольник сопротивлений при ин дуктивной нагрузке.

При последовательном соединении резистора, катушки индуктивности и конденсатора (рисунок 2.3.) общий ток, протекающий по цепи, определяют по закону Ома для цепи переменного тока:

.

где Z – полное электрическое сопротивление электрической цепи.

Индуктивное и емкостное сопротивления создают разность фаз между током и напряжением. Из треугольника сопротивлений угол 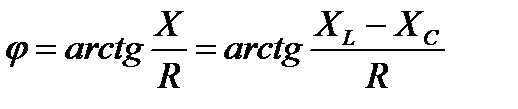. Величина угла и знак его зависят от соотношения между индуктивным Х_Lи емкостным Х_Cсопротивлениями цепи.

1. Х_L> Х_C. Реактивное сопротивление Х=Х_L -Х_Cявляется индуктивным и выражается положительным числом. Угол φ имеет положительное значение (рис. 6-4). Ток отстает от напряжения.

2. Х_L< Х_C. Реактивное сопротивление Х=Х_L -Х_Cявляется емкостным и выражается отрицательным числом. Угол φ имеет отрицательное значение. Ток опережает напряжение (рис. 6-5).

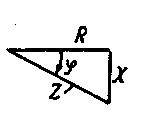
6-5Треугольник напряжений н треугольник сопротивлений; при емкостной нагрузке.

Если стороны треугольника напряжений (рис, 8-7) умножить на вели­чину тока (или стороны треугольника сопротивлений на квадрат тока I²), то получим подобный ему треугольник – треугольник мощностей.

8-7. Треугольники сопротивлений, напряжений и мощностей

В нем горизонтальный катет – активная мощность: 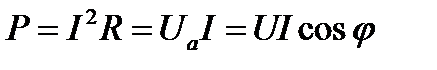, Вт

где I_а - ток протекающий через активное сопротивление R;

U_а – активная составляющая напряжения;

cosj - угол сдвига фаз между током, протекающим по цепи и напряжением.

Ваттметры показывают активную мощность электрической цепи.

Вертикальный катет – реактивная мощность: . Измеряется эта величина в варах (вольт-ампер реактивный).

Гипотенуза треугольника получила название полной мощности:

.

Эта величина измеряется в вольт-амперах (ВА).

Из треугольника мощностей следуют соотношения:

,

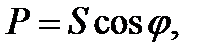
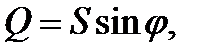
Треугольники сопротивлений, напряжений и мощностей дают наглядное представление о соотношении между тремя величинами. Коэффициент мощности можно определить из любого треугольника:

.

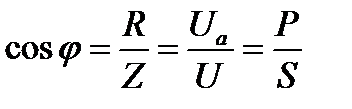Коэффициент мощности характеризует степень использования мощности

Резонанс в последовательной цепи.

Практический интерес представляет равенство индуктивного сопротивления катушки X_L и емкостного сопротивления конден сатора Х_с.. В этом случае полное сопротивление Z становится чисто активным:

Угол φ = 0 и ток I= U/R в цепи совпадает по фазе с напряжением U, электрическая цепь потребляет лишь активную мощность Р= S.Ток в этот момент максимален и может достигать значительной величины, напряжения на элементах U_L и U_с также значительны и при X_L = Х_с>> Rмогут во много раз превышать напряжение питания электрической цепи.

Таким образом, условие резонанса напряжений — равенство индуктивной и емкостной составляющих сопротивления цепи X_L = Х_с,а следствие — наибольший ток в цепи, потребление цепью чисто активной мощности, равные и значительные величины напряжения на реактивных элементах. Наиболее просто резонанс напряжений достигается за счет изменения емкости С при постоянных индуктивности L. При неизменных значениях L и C можно получить резонанс напряжений, меняя частоту питающего напряжения. Резонанс наступит при частоте f_рез=f₀, когда

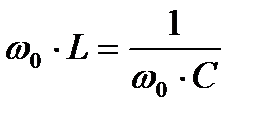
отсюда ;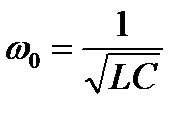

Векторная диаграмма цепи при резонансе показана на рисунке 2.2.

Очевидно, что при X_L=Xc падение напряжений на этих элементах тоже равны U_L=U_C.Тогда U=U_R+U_L+U_C=IR.

Коэффициент мощности при резонансе: cos =1, реактивная мощность цепи равна нулю, т.е. Q=Q_L-Q_C=0, а полная мощность S равна активной мощности P.

U_Lрез

U_Cреззз

U

I

U_R=IR

U_Cрез

Рисунок 2.2. Векторная диаграмма при резонансе напряжений.

Резонанс напряжений характеризуется рядом существенных факторов.

1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т. е. , так как при этом X_L=X_C.

2. Из этого следует, что при неизменном напряжении питающей сети (U=const) при резонансе напряжений ток в цепи достигает наибольшего значения. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки. При малом значении активного сопротивления ток может достигать большого значения.

3. Коэффициент мощности при резонансе cosφ=cos(φ_u-φ_i)= =P/S=R/Z=R/R=l,. т. е. принимает наибольшее значение, кото­рому соответствует угол φ=0. Это означает, что вектор тока и вектор напряжения U сети при этом совпадают по направлению, так как они имеют равные начальные фазы φ_u =φ_i

4. Активная мощность при резонансе Р=RI² имеет наибольшее значение, равное полной мощности S, в то же время реактивная мощность цепи Q=XI ²=(X_L –X_C)I² оказывается равной нулю: Q=Q_L - Q_C =0. При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности Q_L –Q_C =X_LI² = X_CI² могут приобретать теоретически весьма большие значения, в зависимости от значений тока и реактивных сопротивлений.

5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными U_C= U_L= X_CI = X_LI² и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т. е. Ur=U.

Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике и электронике в различного рода приборах и устройствах, основанных на резонансном явлении.

Дата добавления: 2015-08-17