Расчет обделок кругового очертания

Обделки кругового очертания из монолитного бетона или же­лезобетона, а также сборные обделки с постоянными связями растяжения между элементами рассчитывают по схеме упругого кольца в упругой или податливой среде.

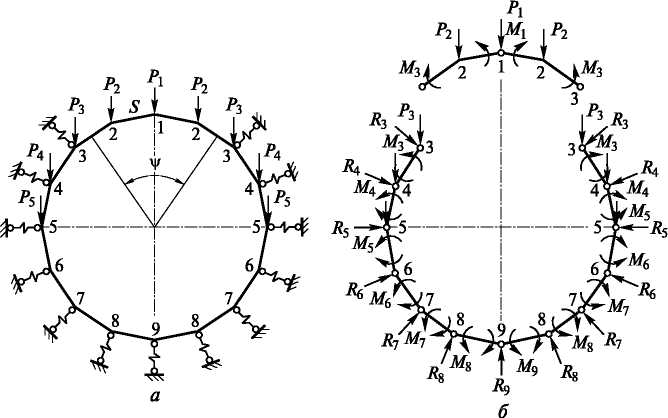
Первая схема — «кольцо в упругой среде» — реализуется при заложении тоннеля в грунтах, обладающих упругими свойствами. Наибольшее распространение получил метод Метропроекта, при помощи которого можно рассчитывать обделки практически лю­бого очертания. При этом круговое очертание обделки заменяют вписанным многоугольником, а распределенные нагрузки — со­средоточенными силами, прикладываемыми в вершинах много­угольника.

Действие сплошной упругой среды имитируют системой упру­гих стержней, которые располагают во всех вершинах многоуголь­ника, кроме тех, которые находятся в безотпорной зоне, опреде­ляемой центральным углом *Р от 90 до 150° (рис. 29.5, а).

Расчет ведут методом сил, принимая основную систему путем врезания шарниров во все вершины, находящиеся в зоне дей­ствия упругого отпора и в замковом сечении и прикладывая в этих сечениях изгибающие моменты, которые принимают за не­известные (рис. 29.5, б). Их определяют путем решения системы линейных алгебраических уравнений (для 16-угольника — 8 урав­нений), которые удобно представить в матричной форме:

АХ + А_р=0, (29.14)

где А — матрица единичных перемещений основной системы; X — вектор неизвестных; д — вектор грузовых перемещений основ­ной системы.

Рис. 29.5. Расчетная схема (а) и основная система {б) при расчете обдел­ки методом Метропроекта

Матрицу А и векторы 1 и А, можно записать в виде

А =

(29.15)

5з1§33 §39	; х =	мъ	■А	А3р
§91§93 §99		м9		'А"9'р'

Единичные и грузовые перемещения определяют по разверну­той формуле Мора с учетом стержневого характера системы:

Е1

N№5

¹ ЕЕ

(29.16)

Е1

ЕЕ

где М_г, М_к, М_р, #,, Ы_к, Ы_р — моменты и нормальные силы от

действия единичных неизвестных и от нагрузки; Д, К_к, К_р — уп­ругие реакции от действия единичных моментов и от нагрузки; /, Р — осредненные моменты инерции и площади поперечного се­чения стержней, являющихся сторонами многоугольника; В — приведенная жесткость упругой опоры, В = кЫ; к — коэффици­ент упругого отпора грунта; Ъ — ширина кольца обделки; * — длина стороны многоугольника.

Усилия в основной системе находят от каждого действия: р; #; М_х=\; М_ъ = 1,..., М₉ = 1 из уравнений равновесия трехшар-нирной арки и последовательно вырезаемых узлов шарнирной цепи.

В результате решения системы канонических уравнений опре­деляют значения моментов, нормальных сил и упругих реакций по формулам:

М = М_р+^М₁М_к; # = #_р+ХДМь К = К_р+^К₁М_к, (29.17)

где М_к — значение неизвестных.

Метод Метропроекта отличается универсальностью, четкостью расчетной схемы, наглядностью и возможностью повышать то­чность расчета. Имеются компьютерные программы расчета обде­лок этим методом, позволяющие быстро получать искомые ре­зультаты при задании конкретных исходных параметров.

Обделки тоннелей, заложенных в неустойчивых водонасыщен-ных грунтах, не оказывающих сопротивления перемещениям кон­струкции, рассчитывают по схеме «кольцо в податливой среде» без учета упругого отпора грунта только на активные нагрузки (рис. 29.6, а).

Реакцию основания р_о принимают в виде равномерно распре­деленной нагрузки, равной сумме вертикального давления грунта и воды и собственного веса кольца обделки. Расчет ведут методом сил, принимая основную систему в виде полукольца, закреплен­ного в нижнем сечении (рис. 29.6, б). Неизвестные усилия Х_{ и Х₂ прикладывают в упругом центре, который для обделок постоян­ной жесткости совпадает с центром кольца. Уравнения деформа­ции имеют следующий вид:

(29.18)

5_пХ_{ + А_1р = 0; д₂₂Х₂ + А_2р = 0.

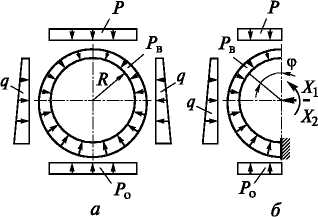
Рис. 29.6. Расчетная схема (а) и основная система (б) «кольца в податли­вой среде»

Перемещения 5_И, 8₂₂, А_1р, А_2р определяют по одночленной формуле Мора. Окончательные усилия в сечениях кольца:

М = М_р + Х_{ - Х₂К сок (р; N = Ы_р + Х₂со8(р.

(29.19)

Для расчета сборных обделок разработаны методы, учитыва­ющие деформации в стыках между элементами.

Дата добавления: 2015-08-17