Властивості спряжених операторів.

Наступні властивості спряжених операторів витікають безпосередньо з визначення.

1) Оператор - лінійний.

2) .

3) Якщо k – число, то .

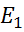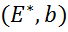Якщо – неперервний лінійний оператор з в , то – неперервний оператор з в .

Якщо – банахові простори, то це твердження може бути точнішим.

Наслідок із теореми Хана-Банаха: Якщо – не нульовий елемент у нормованому просторі , то існує такий неперервний лінійний функціонал 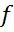на , що

і .

Теорема: Якщо – обмежений лінійний оператор, що відображає банаховий простір в банаховий простір 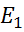, то

.

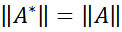Дата добавления: 2015-08-17