Спряжені простори. Приклади

Лекція 13-2

Тема: " Спряжені простори та оператори. Їх властивості. Приклади ".

Дисципліна: "Функціональний аналіз".

Викладач Гусарова І.Г.

Харків, 2014

Мета лекції: Вивчення спряжених просторів та операторів, розглядання їх прикладів та властивостей.

Зміст

Спряжені простори. Приклади

Спряжені оператори

Література

1. Колмогоров, А.Н. Элементы теорий функций и функционального анализа [Текст] / А.Н. Колмогоров, С.В. Фомин. ­­– М.: Физматлит, 2004.

2. Люстерник, Л.А. Краткий курс функционального анализа [Текст] / Л.А. Люстерник В.И. Соболев– М., 2009.

3. Тевяшев А.Д. Функціональний аналіз у прикладах та задачах[Текст] / Тевяшев А.Д.,Головко Н.А.- Навч.посібник.-Харків:ХТУРЕ,1998.

4. Кириллов А.А. Теоремы и задачи функционального анализа[Текст] / Кириллов А.А., Гвишнани А.Д. – М.: Наука, 1988.

5. Вулих, Б.З. Введение в функциональный анализ [Текст] / Б.З. Вулих. ­­–Изд. 2, перераб. и доп. – М., 1967.

6. Князев, П.Н. Функциональный анализ [Текст] / П.Н. Князев– Изд. 2, перераб. М., 2003.

Базові Поняття та Ключові слова:

Лінійний функціонал

Лінійний оператор

Обмежений оператор

Нормований простір

Повний простір

Банаховий простір

Гільбертовий простір

Базис

Ізометричне відображення

Нерівність Гельдера

Гільбертовий простір

Спряжений простір

Спряжений оператор

Норма функціонала

Тема: Спряжені простори та оператори. Їх властивості. Приклади

Спряжені простори. Приклади

Для лінійних функціоналів можна визначити операції додавання та множення їх на числа. Нехай ƒ₁ і ƒ₂ два лінійних функціонала в деякому лінійному просторі E.

Означення. Їх сумою ƒ₁+ƒ₂ називається лінійний функціонал

.

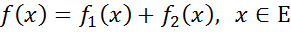Означення. Добутком αƒ₁ лінійного функціонала ƒ₁ на число α називається функціонал

.

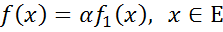Рівності, що визначають ƒ₁+ƒ₂ і 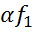можна записати так:

, .

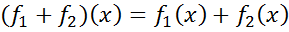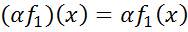Зрозуміло, що сума ƒ₁+ƒ₂ і добуток αƒ₁ представляють собою лінійні функціонали. Крім того, якщо простір E метричний, то з неперервності функціоналів ƒ₁ і ƒ₂ слідує, що ƒ₁+ƒ₂ та αƒ₁ також неперервні на E.

Можна перевірити, що таким чином визначені операції додавання функціоналів та множення їх на число задовольняють всім аксіомам лінійного простору.

Означення. Сукупність всіх неперервних лінійних функціоналів, визначених на деякому лінійному метричному просторі E, утворює лінійний простір. Він називається простором, спряженим з E, та позначається E*.

Нехай початковий простір E нормований. Для неперервних лінійних функціоналів, заданих у нормованому просторі, ми ввели поняття норми, поклавши

Ця величина задовольняє всім аксіомам норми та умовам, які містяться в означенні нормованого простору. Дійсно,

1) 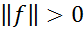, для будь-якого ненульового лінійного функціонала ƒ, ,

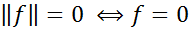2) ,

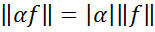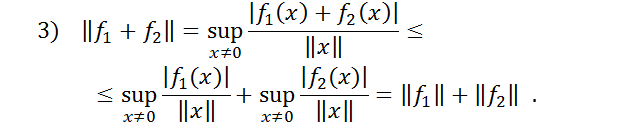
Означення. Таким чином, простір E*, спряжений до нормованого простору, є нормованим простором.

Якщо ми бажаємо підкреслити, що E* розглядається як нормований простір, замість E* іноді пишуть (E*, ).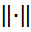

Теорема. Спряжений простір (E*, 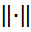) є повним простором.

Доведення. Нехай 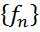‑ фундаментальна послідовність лінійних функціоналів. Тоді для кожного ε >0 знайдеться таке N, що 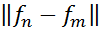< ε, для 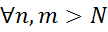. Звідси для 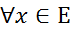виходить

,

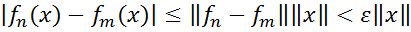тобто, для 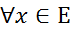числова послідовність 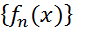фундаментальна, простір 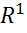– повний, як наслідок 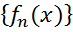- збігається.

Покладемо

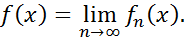
Перевіримо, що ƒ представляє собою неперервній лінійній функціонал. Лінійність перевіряється безпосередньо:

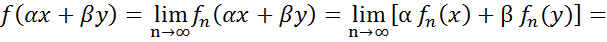
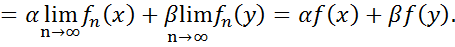
Для доведення неперервності функціонала повернемося до нерівності 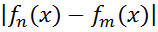< ε 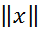і перейдемо в ньому до границі при 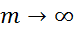, отримаємо

.

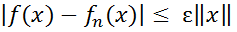Звідси випливає, що функціонал 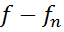обмежений. Але тоді обмежений, а значить і неперервний також функціонал .

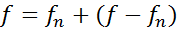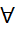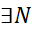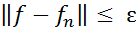Крім того, звідси слідує, що для ε >0 : для 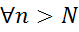, тобто 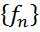збігається до .

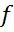Підкреслимо, що ця теорема слушна незалежно від того, чи є початковий простір E повним.

Дата добавления: 2015-08-17