Спряжені оператори

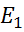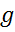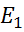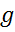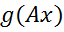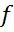Розглянемо неперервний лінійний оператор , котрий відображає лінійний метричний простір в такий же простір . Нехай – лінійний функціонал, визначений на , Застосуємо функціонал до елемента ; легко перевірити, що є неперервним лінійним функціоналом, визначеним на ; позначимо його . Таким чином, функціонал 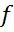є елементом простору . Кожному функціоналу ми поставили в відповідність функціонал , тобто отримали деякий оператор, що відображає 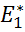в . Цей оператор називається спряженим до оператора и позначається , тобто .

Означення: Позначивши значення функціоналу 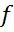на елементі символом , отримаємо, що

, або ,

це співвідношення приймається за означення спряженого оператора.

Тобто

Означення: Оператор діючий з 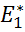в , такий що називається оператором, спряженим до оператора 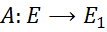, де

.

Дата добавления: 2015-08-17