
Читайте также:
|
1. Нехай E – 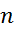 -вимірний лінійний простір (дійсний або комплексний). Оберемо в ньому який-небудь базис
-вимірний лінійний простір (дійсний або комплексний). Оберемо в ньому який-небудь базис 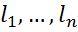 ; тоді будь-який елемент
; тоді будь-який елемент 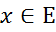 однозначно представляється у вигляді
однозначно представляється у вигляді

Якщо 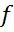 – лінійний функціонал на E, то ясно, що
– лінійний функціонал на E, то ясно, що

отже, лінійний функціонал однозначно визначається своїми значеннями на векторах базису 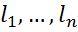 , причому ці значення можна задати довільно. Визначимо лінійні функціонали
, причому ці значення можна задати довільно. Визначимо лінійні функціонали  , вважаючи
, вважаючи
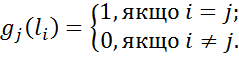
Очевидно, що ці функціонали лінійно-незалежні. Ясно, що 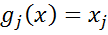 , тому формулу (2) можна записати у вигляді
, тому формулу (2) можна записати у вигляді
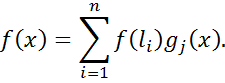
Таким чином, функціонали  складають базис у просторі E*, тобто E* –
складають базис у просторі E*, тобто E* – 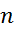 -вимірний лінійний простір, базис
-вимірний лінійний простір, базис  в E* називають двоїстим по відношенню до базису
в E* називають двоїстим по відношенню до базису  в E.
в E.
Різні нормі в просторі E породжують різні норми в E*. Ось декілька прикладів пар відповідних один одному в E і E*:
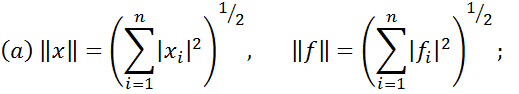



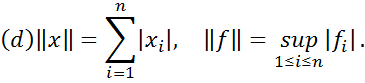
В цих формулах  – це координати вектора
– це координати вектора  в базисі
в базисі 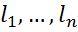 , а
, а  – координати функціонала
– координати функціонала  E* в двоїстому базисі
E* в двоїстому базисі 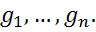
2. Розглянемо простір c0 послідовностей
 що збігаються до нуля з нормою
що збігаються до нуля з нормою

Покажемо, що спряжений до нього простір ( ) ізоморфний простору
) ізоморфний простору  абсолютно підсумованих послідовностей
абсолютно підсумованих послідовностей  з нормою
з нормою
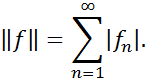
Будь-яка послідовність  визначає в просторі c0 лінійний обмежений функціонал
визначає в просторі c0 лінійний обмежений функціонал 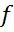 за формулою
за формулою

такий що
 (3)
(3)
Ясно, що

тому

Розглянемо в c0 вектори
 ;
;
 ;
;
…………………………
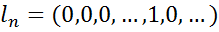 ;
;
……………………….
і покладемо

(якщо  , то вважаємо, що
, то вважаємо, що  ). Тоді
). Тоді  ,
,  і
і

так, що
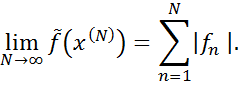
Внаслідок цього 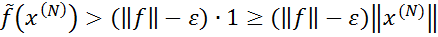 ,
,

В силу довільності  , тобто
, тобто

зіставляючи з доведеною вище протилежною нерівністю, робимо висновок, що

Таким чином, ми побудували лінійне ізометричне відображення  простору
простору  в простір
в простір  . Залишилось впевнитися в тому, що образ простору
. Залишилось впевнитися в тому, що образ простору  співпадає з усім
співпадає з усім  , тобто що будь-який функціонал
, тобто що будь-який функціонал  можна подати у вигляді (3), де
можна подати у вигляді (3), де  . Для будь-якого
. Для будь-якого  маємо
маємо

причому ряд, що стоїть праворуч, збігається у  до елемента
до елемента  , бо
, бо

Так як функціонал  неперервний, то
неперервний, то

тому достатньо перевірити, що
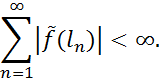
Вважаючи, що

і вважаючи, що  ,
,  , маємо
, маємо

звідки в силу довільності  робимо висновок, що
робимо висновок, що

3. Неважко довести, що простір  , спряжений з простором
, спряжений з простором  , ізоморфний простору
, ізоморфний простору  , що складається з усіх обмежених послідовностей
, що складається з усіх обмежених послідовностей 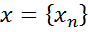 з нормою
з нормою

4. Нехай 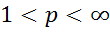 и
и  – простір всіх послідовностей
– простір всіх послідовностей 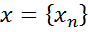 , для яких
, для яких

Можна довести, що спряжений до нього простір 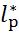 ізоморфний до простору
ізоморфний до простору  ,
,  . Загальний вигляд неперервного лінійного функціонала на
. Загальний вигляд неперервного лінійного функціонала на  :
:

Доведення засноване на використанні нерівності Гельдера.
5. З’ясуємо структуру простору, спряженого до гільбертового.
Теорема: Нехай  – дійсний гільбертовий простір. Для будь-якого неперервного лінійного функціонала
– дійсний гільбертовий простір. Для будь-якого неперервного лінійного функціонала 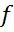 на
на  існує єдиний елемент
існує єдиний елемент  , такий що
, такий що
 , (4)
, (4)
причому  . Обернено, якщо
. Обернено, якщо  , то формула (4) визначає такий неперервний лінійний функціонал
, то формула (4) визначає такий неперервний лінійний функціонал 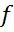 , то
, то  . Таким чином, рівність (4) визначає ізоморфізм
. Таким чином, рівність (4) визначає ізоморфізм  між просторами
між просторами  .
.
Дата добавления: 2015-08-17; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Спряжені простори. Приклади | | | Спряжені оператори |