Исследование структурных изменений с помощью теста Чоу

Как было показано выше, при разных значениях фиктивной переменной получаются разные уравнения регрессии. Целесообразность применения двух уравнений регрессии вместо одного можно оценить, не прибегая к вводу фиктивных переменных. Для этого используется тест Чоу.

Пусть имеется n наблюдений, позволяющих охарактеризовать зависимость результата от одного или нескольких количественных факторов. У исследователя есть основания предполагать, что совокупность неоднородна с точки зрения числовых характеристик воздействия факторов на результат. Предполагается также, что однородность может быть достигнута, если совокупность разбить по определенному критерию на 2 части.

Для проверки этих предположений находят параметры 3 уравнений регрессии. Первое уравнение строится для всей совокупности наблюдений, второе и третье – для соответствующих выделенных подмножеств совокупности наблюдений. Для каждого из этих уравнений находят остаточную сумму квадратов SS _ост:

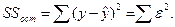
Обозначим остаточную сумму квадратов для общего уравнения регрессии через SS ₀, для уравнений регрессии по подмножествам наблюдений – через SS ₁ и SS ₂.

Тогда равенство выполняется, если параметры всех трёх функций совпадают.

В противном случае 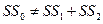. Чем больше разница между двумя частями этого неравенства, тем больше различия между двумя подмножествами с точки зрения параметров уравнений регрессии. Существенность различий проверяют с помощью F -критерия.

Фактическое значение F -критерия находят по формуле:

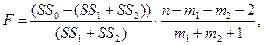
где m ₁и m ₂ – количество параметров (без свободного члена) в уравнениях, построенных по подмножествам, n – число наблюдений по всей совокупности.

Табличное значение F -критерия находят для степеней свободы df ₁= m ₁+ m ₂+1 и df ₂= n - m ₁- m ₂-2. Если фактическое значение окажется больше табличного, то имеют место структурные сдвиги и целесообразно строить уравнение регрессии с соответствующей переменной.

Применение теста Чоу рассмотрим на примере, в котором исследовалась зависимость стоимости проезда от расстояния и типа поезда.

Нам необходимо найти параметры уравнения

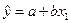
для массивов данных:

- для всех данных (n =30);

- для данных о стоимости проезда в электричках (n =17);

- для данных о стоимости проезда в поездах дальнего следования (n =13).

Применяя МНК к данным таблицы 3, получим следующие уравнения регрессии и значения сумм квадратов остатков:

- по всем типам поездов:

- для проезда в электричках:

- для проезда в поездах дальнего следования:

Фактическое значение F -критерия равно

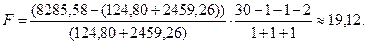
Табличное значение F -критерия равно 2,98 (при α=0,05 и степенях свободы df ₁=1+1+1=3 и df ₂=30-1-1-2=26).

Так как фактическое значение F -критерия больше табличного, следует признать существенность различия характеристик зависимости стоимости проезда от расстояния для разных типов поездов. Следовательно, для каждого типа поезда следует строить своё уравнение регрессии или объединить их в одно, используя фиктивную переменную (что и было сделано выше).

Тест Чоу можно использовать также, если исследуется зависимость уровня ряда от времени, т.е. строится уравнение тренда вида . В этом случае деление совокупности наблюдений на две части производится относительно определённого момента времени, в который, по мнению исследователя, произошли какие-либо структурные изменения.

Контрольные вопросы

1. Можно ли учесть в уравнении регрессии неколичественные факторы? Каким образом?

2. Дайте определение фиктивной переменной.

3. Сколько фиктивных переменных нужно ввести, если имеются 2 качественных фактора, причём один из них имеет три возможных значения, а другой – два?

4. Как интерпретируется коэффициент регрессии при фиктивной переменной сдвига?

5. Как интерпретируется коэффициент регрессии при фиктивной переменной наклона?

6. Каков общий вид модели регрессии с одной количественной и одной фиктивной переменной?

7. В какой модели (моделях) с фиктивными переменными учитывается различие влияния количественных факторов на результат при разных значениях качественного фактора?

8. Назовите достоинства и недостатки моделей с фиктивными переменными.

9. Какова область применения теста Чоу?

10. Какие показатели сравниваются между собой по тесту Чоу? Какой статистический критерий в этом случае используется? Опишите методику применения теста Чоу.

Дата добавления: 2015-08-20