Общий вид модели регрессии с фиктивными переменными

Модели, рассмотренные выше, можно считать частными случаями общей модели. Очевидно, что это будет модель, в которой при разных значениях фиктивной переменной будут разные параметры. Например, для простейшего случай с одним количественным фактором (x ₁) и одной фиктивной переменной (z ₁₁) необходимо объединить в одну модель 2 уравнения регрессии:

(15)

(16)

Используем для этого модели (2) и (13):

(17)

Действительно, при

Параметры уравнений (15) и (16) можно выразить через параметры уравнения (17) следующим образом:

Графически модель (17) может быть представлена в виде двух прямых, отражающих зависимость результата от количественного фактора при разных значениях фиктивной переменной. Параметры этих прямых различны, поэтому они имеют разный угол наклона и пересекают ось ординат в разных точках.

Пример. Рассмотрим зависимость стоимости проезда (y, руб.) от расстояния (x ₁, км) и типа поезда (z ₁₁=0, если проезд осуществляется на электричке; z ₁₁=1 – на поезде дальнего следования). Можно ожидать, что характер ценообразования на 2 этих типах поездов полностью различен, т.е. для описания зависимости следует применить модель (17). Исходные данные приведены в таблице 3.

Таблица 3

Стоимость проезда в электричках и поездах дальнего следования из Санкт-Петербурга в зависимости о расстояния и типа вагона

Станция назначения	Расстояние, км	Тип поезда	Стоимость проезда, руб.
Платформа 39 км			45,0
Мга			54,0
Платформа 44 км			54,0
Платформа 47 км			54,0
Платформа 63 км			63,0
Платформа 67 км			72,0
Платформа 69 км			72,0
Платформа 78 км			81,0
Волхов			117,0
Чудово			117,0
Платформа 138 км			135,0
Будогощь			135,0
Приозерск			135,0
Луга			135,0
Платформа 148 км			144,0
Платформа 152 км			144,0
М.Вишера			153,0
Мга			98,1
Волхов			124,9
Чудово			155,2
Приозерск			137,4
Луга			137,4
М.Вишера			145,5
Новгород			198,5
Тихвин			157,6
Пикалево			169,7
Лодейное поле			169,7
Подпорожье			189,8
Псков			189,8
Бологое			227,9

После применения МНК получим следующее уравнение регрессии:

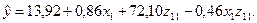(5)

(t _факт) (2,32) (15,76) (75,54) (-6,99)

R ²=0,96 n =30

Табличное значение t-критерия Стьюдента составляет 2,06 при числе степеней свободы df = n – m –1=30–3–1=26 и уровне значимости α=0,05, следовательно, все параметры уравнения регрессии значимы и их можно проинтерпретировать. Коэффициент множественной корреляции свидетельствует о тесной связи между признаками.

Коэффициент b ₁ при факторе x ₁ означает, что если ехать на электричке (z ₁₁=0), то при увеличении расстояния на 1 км стоимость проезда увеличивается в среднем на 0,86 руб. Если воспользоваться поездом дальнего следования (z ₁₁=1), то стоимость 1 км в среднем будет ниже, чем в электричке (d ₁₁₁=-0,46) на 46 копеек.

Параметр c ₁₁ интерпретируется иначе, чем в модели с фиктивной переменной сдвига (2). Так как прямые (15) и (16) непараллельны, параметр c ₁₁ может рассматриваться только как разница между значениями результата для z ₁₁=1 и z ₁₁=0 при условии, что количественный фактор x ₁ равен нулю.

Для нашего примера можно отметить, что на коротких расстояниях передвижение на поезде дальнего следования обходится дороже, чем на электричке. С увеличением расстояния более выгодно становится пользоваться поездом дальнего следования (стоимость проезда за километр в нём ниже). Точка пересечения прямых (15) и (16) имеет координаты, которые можно проинтерпретировать как расстояние, для которого стоимость проезда на электричке и поезде дальнего следования одинакова.

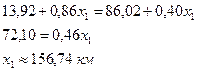
Стоимость проезда на расстояние 156,74 км одинакова как для электричек, так и для поездов дальнего следования и составляет примерно 156 руб. 74 коп. При меньшем расстоянии выгоднее пользоваться электричкой, при большем – поездом дальнего следования.

При достаточном числе наблюдений (не менее 7 на каждый параметр уравнения регрессии, кроме свободного члена) модель (17) может быть использована на первом шаге при изучении влияния качественного фактора на результат. Незначимость отдельных параметров этой модели свидетельствует о необходимости перехода к моделям (2), (13) или к модели без данного фактора.

Модели (2), (13), (17) были построены для простейшего случая с двумя факторами: одной фиктивной переменной и одной количественной переменной. Запишем каждую из них в общем виде:

1. Модель с фиктивными переменными сдвига:

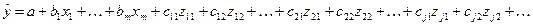(18)

где a – свободный член;

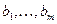– коэффициенты при количественных факторах ;

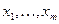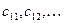– коэффициенты при фиктивных переменных , созданных для первого качественного признака-фактора;

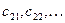– коэффициенты при фиктивных переменных 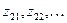, созданных для второго качественного признака-фактора;

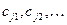– коэффициенты при фиктивных переменных , созданных для j -го качественного признака-фактора.

2. Модель с фиктивными переменными наклона:

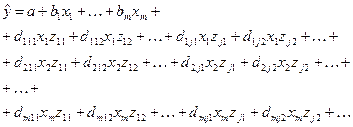(19)

Для удобства чтения уравнение (19) записано в несколько строк. В первой строке приведено обычное уравнение множественной регрессии с количественными факторами 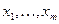. Другие строки, начиная со второй, содержат (с параметрами d) попарные произведения количественных факторов на фиктивные переменные.

3. Общая форма модели с фиктивными переменными объединяет модели (18) и (19):

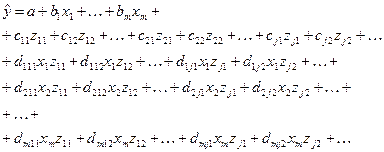(20)

Частным случаем модели с фиктивными переменными является модель, не содержащая количественных факторов. Рассмотрим этот вид моделей на примере модели с одной фиктивной переменной (z ₁₁). Очевидно, что здесь не может быть фиктивной переменной наклона, так как отсутствует количественный фактор. Поэтому это может быть только модель с фиктивной переменной сдвига:

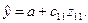(21)

Так как фиктивная переменная принимает всего два значения, может быть рассчитано всего два выровненных значения результата: при z ₁₁=0 и при z ₁₁=1. Это будут соответственно величины a и (a + с ₁₁). Их можно рассматривать как средние значения результата по группам, образованным двумя значениями фиктивной переменной.

Существенным недостатком моделей с фиктивными переменными является значительное число параметров, требующее соответствующего увеличения числа наблюдений.

Избежать этого можно путём объединения нескольких значений качественного фактора одним, если эти значения не различаются по силе влияния на результат.

Модели с фиктивными переменными могут применяться для анализа временных рядов, в частности для изучения периодических колебаний. Если рассматриваются сезонные колебания продаж (например, прохладительных напитков), можно построить модель зависимости объёма продаж от квартала, месяца и т.п. Чем шире будет интервал времени, рассматриваемый в качестве фактора, тем короче будет модель, что повышает её статистическую надёжность. Однако слишком широкие интервалы ведут к значительному усреднению характеристик влияния качественного фактора, что снижает аналитическую ценность модели.

Дата добавления: 2015-08-20