Модели регрессии с фиктивными переменными сдвига

Рассмотрим в качестве уравнения регрессии линейную функцию. Для простоты возьмём в качестве факторов одну количественную переменную (x ₁) и одну фиктивную переменную (z ₁₁):

(2)

Из этого уравнения следует, что при z₁₁=1 результат (y) равен

(3)

а при z ₁₁=0 результат (y) равен

(4)

Два полученных уравнения (3) и (4) различаются величиной свободного члена. То есть для одного значения качественной переменной уровень результата всегда в среднем будет на с ₁₁ единиц выше или ниже, чем для другого.

Графически эта ситуация соответствует двум параллельным прямым. Коэффициент b ₁ при количественном факторе остается неизменным, т.е. изменение фактора x ₁ оказывает одинаковое влияние на результат при разных значениях качественного фактора.

Так как изменение значения фиктивной переменной в модели (2) приводит к изменению значения результата на некую среднюю величину, не зависящую от значений количественного фактора, такую переменную еще называют фиктивной переменной сдвига. Изменение ее значения приводит к переходу от одной параллельной прямой к другой.

Пример. Рассмотрим в качестве результата стоимость изготовления металлической двери (y, тыс. руб.), в качестве количественного фактора – площадь дверного полотна (x ₁, м²), в качестве неколичественного фактора (z ₁₁) – страну-изготовителя замка. С некоторым допущением разделим все дверные замки на 2 группы: отечественные (более дешёвые) и импортные (более дорогие). Фиктивная переменная будет описана как

Будем считать, что остальные факторы, оказывающие влияние на стоимость двери (дверные глазки, декоративная отделка, дополнительные пластины усиления и т.д.), являются одинаковыми для всех дверей. Исходные данные приведены в таблице 1.

Таблица 1

Стоимость металлической двери в зависимости от площади дверного полотна и типа замка

Площадь дверного полотна, м^2	Тип замка	Стоимость двери, тыс. руб.
1,6		16,656
1,6		17,126
1,6		17,600
1,8		18,463
1,8		17,524
1,8		18,449
1,9		19,352
1,9		19,920
1,9		20,456
2,2		22,051
2,2		22,683
2,2		23,337
2,3		22,952
2,3		23,614
2,3		24,291
2,5		24,752
2,5		25,485
2,5		26,193
1,6		19,672
1,6		20,131
1,6		20,593
1,8		21,465
1,8		20,569
1,8		21,508
1,9		22,387
1,9		22,915
1,9		23,495
2,2		25,076
2,2		25,703
2,2		26,351
2,3		25,979
2,3		26,672
2,3		27,319
2,5		27,766
2,5		28,515
2,5		29,236

После применения МНК к уравнению (2) получим:

(5)

(t _факт) (2,05) (30,03) (15,20)

Табличное значение t-критерия Стьюдента составляет 2,04 при числе степеней свободы df = n – m –1=36–2–1=33 и уровне значимости α=0,05. Следовательно, все параметры уравнения регрессии значимы, т.е. оба фактора оказывают значимое воздействие на результат. Коэффициент множественной корреляции свидетельствует о тесной связи между признаками.

Проинтерпретируем параметры полученного уравнения регрессии.

Коэффициент b ₁ при факторе x ₁ равен 9,649, следовательно, при увеличении площади дверного полотна на один квадратный метр её стоимость в среднем возрастает на 9,649 тыс. руб. при условии, что страна-производитель замка не меняется.

Коэффициент c ₁₁ при фиктивной переменной равен 3,025, следовательно, дверь с импортным замком в среднем на 3,025 тыс. руб. дороже двери с отечественным замком при одной и той же площади дверного полотна.

Подставляя значение фиктивной переменной z ₁₁=0, получим уравнение зависимости стоимости двери от её площади при условии, что замок отечественный, z ₁₁=1 – то же уравнение для двери с импортным замком:

(6)

(7)

Отметим, что если находить параметры этих уравнений регрессии отдельно, применяя к исходным данным МНК, получим аналогичный, но не совсем такой результат.

Так, после применения МНК к исходным данным для дверей с отечественными замками уравнение регрессии имеет вид:

(8)

Применение МНК к исходным данным для дверей с импортными замками приводит к следующему результату:

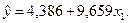(9)

Различие параметров моделей (6), (7) и (8), (9) объясняется тем, что на стоимость дверей оказывают воздействие случайные факторы (колебания курса валют, разные расценки у фирм-производителей). Поэтому минимизация квадратов случайных отклонений в целом по совокупности и по отдельным ее частям приводит к разным результатам.

Дата добавления: 2015-08-20