Модели регрессии с фиктивными переменными наклона

Рассмотрим другую ситуацию: коэффициент регрессии при количественном факторе зависит от значения фиктивной переменной:

(10)

(11)

(12)

В таком случае говорят, что имеют место структурные изменения в исследуемой зависимости. Для их учёта в уравнении регрессии фиктивную переменную вводят как сомножитель при количественной переменной (так как параметр d объединяет две переменные, он имеет тройной индекс d ₁₁₁):

(13)

Действительно, если рассмотреть это уравнение для z ₁₁=0 и z ₁₁=1, то получим:

Следовательно, коэффициент b ₁₂ из модели (11) будет равен (b ₁₁+ d ₁₁₁).

Графически модель (13) можно представить в виде двух прямых с разным углом наклона, отражающих зависимость результата от количественного фактора при разных значениях фиктивной переменной. Её называют фиктивной переменной наклона, так как при включении в модель регрессии она позволяет изменить угол наклона прямой.

Соответственно параметр b ₁ интерпретируется как сила влияния количественного фактора при одном значении качественной переменной (для которого z ₁₁=0), а параметр d ₁₁₁ – как среднее изменение силы влияния количественного фактора при переходе от одного значения качественной переменной к другому (для которого z ₁₁=1).

Пример. Рассмотрим зависимость стоимости проезда в поездах дальнего следования (y, руб.) от расстояния (x ₁, км) и типа вагона (плацкартный или купейный). Очевидно, что стоимость проезда в вагонах разного типа отличается, но эта разница зависит от расстояния. Так как в плацкартном вагоне места всегда дешевле, примем его за базу (z ₁₁=0). Исходные данные приведены в таблице 2.

Таблица 2

Стоимость проезда в поезде дальнего следования из Санкт-Петербурга в зависимости от расстояния и типа вагона

Станция назначения	Расстояние, км	Тип вагона	Стоимость проезда, руб.
Мга			98,1
Волхов			124,9
Будогощь			133,4
Приозерск			137,4
Луга			137,4
М.Вишера			145,5
Тихвин			157,6
Пикалево			169,7
Подпорожье			189,8
Псков			189,8
Бологое			227,9
Петрозаводск			229,2
Осташков			249,3
Вел. Луки			308,9
Вологда			463,4
Ярославль			349,6
Тула			687,0
Владимир			458,0
Мга			313,4
Волхов			384,2
Будогощь			404,4
Приозерск			414,6
Луга			414,6
М.Вишера			435,5
Тихвин			465,8
Пикалево			495,3
Подпорожье			547,3
Псков			547,3
Бологое			643,3
Петрозаводск			648,4
Осташков			697,4
Вел. Луки			850,5
Вологда			1275,2
Ярославль			950,7
Тула			1834,8
Владимир			1223,5

Применим МНК к модели (13):

Подставим в систему исходные данные:

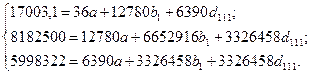
В результате решения системы нормальных уравнений получим следующую модель:

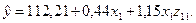(14)

(t _факт) (2,93) (4,31) (11,40)

Табличное значение t -критерия равно 2,04 (α=0,05, df = n – m –1=36–2–1=33), следовательно, все найденные параметры уравнения регрессии значимы. Это подтверждает нашу гипотезу о том, что прирост стоимости проезда на 1 км различен для плацкартных и купейных вагонов. Теснота связи между результатом и факторами высокая (R =0,942).

Параметр b ₁, равный 0,44, показывает, что с увеличением расстояния на 1 км стоимость проезда в плацкартном вагоне в среднем увеличивается на 44 копейки. Параметр d ₁₁₁, равный 1,15, показывает, что за каждый дополнительный километр пути за проезд в купейном вагоне нужно заплатить на 1,15 руб. больше, чем в плацкартном. Сумма b ₁ и d ₁₁₁ равна 1,59, следовательно, с увеличением расстояния на 1 км стоимость проезда в купейном вагоне в среднем увеличивается на 1,59 руб.

Дата добавления: 2015-08-20