|
Читайте также: |
Для правильной интерпретации результатов, используют различные статистические методы обработки данных. Одним из наиболее известных является метод наименьших квадратов.
Суть метода – на имеющемся поле распределения случайной величины необходимо найти уравнение линии минимально удаленной от всех экспериментальных точек.
Проблема заключается в том, что одни точки лежат выше необходимой линии, а другие – ниже, и простое суммирование дает в результате ноль.
Для решения этой проблемы суммируют квадраты этих расстояний.
Для того, чтобы разброс был минимальным необходимо выполнение условия:
 |
Очевидно, что
Тогда получим m уравнений вида
 | |||
 |
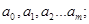из которых определим
Уравнений получится столько, сколько неизвестных коэффициентов необходимо определить.
Рассмотрим применение метода наименьших квадратов для линейной модели.
Пусть имеем набор экспериментальных данных вида:
Сумма квадратов отклонений от «истинной» прямой
Дата добавления: 2015-08-20; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ошибки параллельных опытов. Дисперсия параметра оптимизации. Проверка однородности дисперсий. | | | Проверка адекватности модели. Проверка значимости коэффициентов. |