Полный факторный эксперимент типа 2k, его свойства и математическая модель.

При планирование первого порядка в качестве факторов выбираются только контролируемые управляемые факторы (переменные). Обеспечивается возможность независимого изменяемого каждого из факторов и поддерживание его на определенном уровне.

Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В этом случае, если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных сочетаний уровней факторов.

Простая формула, которая для этого используется, N = 2к, где N – число опытов, к – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

ПФЭ – эксперимент, реализующий все возможные неповторяющиеся комбинации уравнений независимых факторов. Основная задача – определить коэффициенты функции отклика. Здесь реализация все возможного сочетания и факторов на двух уровнях 2^k.

ПФЭ позволяет учесть взаимодействие факторов, т.е. вводить в модель произведение всех учитывающих факторов: y=b₀+b₁x₁+b₂x₂+b₃x₁x₂, при этом в матрицу вводится столбец произведения факторов.

x₁ x₂ x₁x₂

+ - -

- - +

- + -

+ + +

Недостаток ПФЭ: с увеличением числа факторов резко растет число экспериментов.

Два свойства следуют непосредственно из построения матрицы. Первое из них – симметричность относительно центра эксперимента – формулируется следующим, образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, или 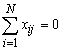, где j – номер фактора, i – номер опыта, N – число опытов.

Второе свойство – так называемое условие нормировки – формулируется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов, или 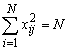. Это следствие того, что значения факторов в матрице задаются +1 и –1.

Сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или. , j¹n.

Это важное свойство называется ортогональностью матрицы планирования.

Последнее, четвертое свойство называется ротатабельностью, т.е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Понятие плана эксперимента. Кодирование факторов. Графическое и табличное представление плана.

Понятие плана эксперимента

Множество всех точек проведения экспериментов можно представить в виде матрицы и называться планом эксперта.

хⁱ = (х₁ⁱ, х₂ⁱ, …, х_nⁱ), i = 1, 2, …, N

x₁₁…x_1k

x₂₁…x_2k

… …

x_n1…x_nk

Помимо табличной записи плана эксперимента существуют и графическое представление. В основе составления плана эксперимента лежат математические основы комбинаторики и т.к. латинский квадрат. Латинский квадрат – таблица n×n, заполняется n различными символами, т.о, чтобы в каждой строке и столбце встречалось n символов по 1 разу.

Используют кодирование факторов: нормализация факторов (преобразование натуральных значений факторов в безразмерный вид): x=(x_n-x_n0)/∆x

Графическое представление плана:

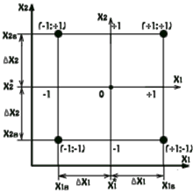
Табличное представление обычно в виде матрицы.

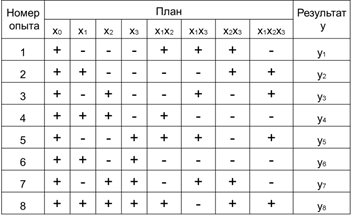
Свойства матрицы

1.Симметричности – алгебраическая сумма элементов вектор-столбца каждого фактора равна 0(кроме свободного члена)

2. Свойство нормирования – сумма квадратов каждого столбца равна числу опытов

3. Свойство ортогональности – скалярное произведение вектор-столбцов равно 0.

Спектр плана - совокупность всех точек плана, отличающихся уравнением хотя бы одного фактора.

Центра плана – точка с координатами, равная средним значениям в каждом столбце.

Центральный план – план, у которого центр находится в начале координат.

Ортогональный план – такой план, у которого информационная матрица является диагностикой.

Свойства ортогонального плана: оценки коэффициентов независимы; исключение незначимого коэффициента не влияет на оценки других коэффициентов.

План называется рототабельным(вращательным), если дисперсия оценки y(x) перемещенной в точку x зависит только от расстояния точки x от центра плана и не зависит от направления полученного уровня регрессии.

План ненасыщенный, если число проведенных экспериментов превысит число оцениваемых коэффициентов.

План насыщенный, если число проведенных экспериментов равно числу оцениваемых коэффициентов.

Дата добавления: 2015-08-20