Параметр оптимизации. Виды параметров оптимизации. Требования к параметру оптимизации.

Эксперимент в науке и производстве. Задачи планирования эксперимента. Основные понятия теории планирования эксперимента.

Эксперимент – метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления действительности. Особенность эксперимента заключ. в том, что он всегда имеет цель и составляет серию опытов.

Опыт – воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации.

Планирование эксперимента дает возможность:

- возможность математического описания процесса;

- разработка стратегии поиска оптимального режима, оптимальных условий протекания процесса;

- минимизация числа опытов;

- одновременное варьирование всех факторов;

- минимизацию ошибок эксперимента;

- выбор стратегии эксперимента.

Различают эксперимент: натурный, модельный, мысленный и компьютерный.

Модельный эксперимент – экпер-т, который ставится на материальных моделях, воспроизводящих существующие черты исследуемой природной ситуации, технического устройства или процесса.

Модельный эксперимент подразделяется на качественный и количественный. Качественный эксп-т устанавливает наличие или отсутствие предполагаемого теорией явления, а количественный – выявляет количественную определенность к-л свойства объекта.

Существуют след. методы проведения экспер-в:

1) пассивный эксперимент - эксперимент, при котором уровни факторов в каждом опыте регистрируются исследователем, но не задаются;

2) активный эксперимент - эксперимент, в котором уровни факторов в каждом опыте задаются исследователем.

Промышленный эксперимент - эксперимент, проводимый в производственных условиях на действующем объекте. В связи с особенностями промышленного экспер-та возникают такие проблемы, как: высокая стоимость, крупномасштабность, ограниченность вариации факторов.

Задачи планирования экспер-та:

1. Измерение величины при фиксированных условиях.

2. Проверка гипотезы.

3. Выяснение механизма явления.

4. Оптимизация.

5. Динамические измерения.

6. Классификация наблюдений или распознавание образцов.

Планирование эксперта - наука о способах составления экономичных экспериментальных планов.

Экспериментальный план должен позволять:

· извлекать максимальную информацию;

· давать представление о способах проведения эксперимента;

· давать представление о способах обработки экспериментальных данных;

· их использование в инженерных расчетах.

Методы планирования экспериментов.

Цель: получение зависимости выходного параметра от выходных факторов y = f(, … 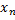), анализ который позволит оценить степень и характер влияния каждого фактора на выходящий параметр, т.е. механизм влияния.

Основные методы: полный факторный эксперимент; дробный факторный эксперимент; латинские, греко-латинские, комбинационные квадраты.

Этапы активного эксперимента: определение цели эксперимента → факторы их уровня → выбор вида модели → построения плана эксперимента → определение параметров модели → выбор вида модели(линейная: y=b₀+∑b_i*x_i, второго порядка: y=b₀+∑b_ix_i+∑b_ij*x_ix_j+∑b_ii*x²). Цель эксперимента определяет вид модели. Вид модели определяет план эксперимента.

Виды планов:

1.При планировании экспериментов применяют планы первого и второго порядков. Планы боле высоких порядков применяются редко из-за вычислительной сложности.

2.Планы первого порядка - планы, которые позволяют провести эксперимент для поиска уравнения регрессии, содержит только первые степени факторов:

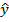=b₀+∑b_i x_i+∑b_iu x_i x_u+∑b_{i ju} x_i x_j x_u…

3.Планы второго порядка – планы, которые позволяют провести эксперимент для поиска уравнения регрессии, содержащие вторые степени факторов:

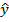=b₀+∑b_i x_i+∑b_ii x_i²+∑b_{i u} x_i x_u+…

Понятия о факторах. Классификация факторов. Требования предъявляемые к факторам, при планировании эксперимента.

При планировании часто используют модель черного ящика:

х₁

х₂ у₁

х₃ у₂

х_1, х_2, х₃ – факторы, у_1, у₂ –отклики (параметры).

Фактор – переменная величина, по предположению, влияющая на результаты экспер-та.

Отклик (параметр) – наблюдаемая случайная переменная, по предположению, зависящая от факторов.

Функция отклика – завис-ть мат. ожидания отклика от факторов.

Уровень фактора – фиксированное значение фактора относительно начала отсчета.

Факторное пространство – пространство, координат. оси которого соответствуют значениям факторов.

Область экспериментирования (область планирования) – область факторного пространства, где могут размещаться точки, отвечающие условиям проведения экспер-та.

В зависимости от шкалы измерения факторы классифицируют:

- номинальные;

- порядковые;

- интервальные;

- относительные.

Номинальные факторы характеризуют качественную классификацию переменных (пол, национальность, цвет, город и т.д.).

Порядковые факторы позволяют ранжировать (упорядочить) объекты, указав, какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной.

Интервальные факторы позволяют численно выразить и сравнить различия между ними (напр, температура).

Относительные факторы – факторы, измеряемые в интервальной шкале, с наличием определенной точкой абсолютного нуля.

Требования, предъявляемые к факторам:

- управляемость;

- операциональность (однозначность);

- точность измерения;

- совокупно совместимы;

- независимость;

Требования, предъявляемые к отклику (параметру):

- параметр должен измеряться при любом изменении (комбинации) фактора;

- параметр должен быть статистически эффективным, то есть измеряться с наибольшей точностью;

- параметр должен быть информационным, то есть всесторонне характеризовать процесс;

- параметр должен иметь физический смысл;

- параметр должен быть однозначным, то есть должно минимизироваться или максимизироваться только одно свойство изделия или процесса.

Параметр оптимизации. Виды параметров оптимизации. Требования к параметру оптимизации.

При планировании эксперимента очень важно определить параметр, который нужно оптимизиро­вать. Цель исследования необходимо сформу­лировать очень четко и допускать количественную оценку. Характеристика цели, заданная коли­чественно, называется параметром оптимизации. Параметр оптимиза­ции является реакцией (откликом) па воздействие факто­ров, которые определяют поведение выбранной сис­темы.

Виды параметров оптимизации

В зависимости от объекта и цели исследования пара­метры оптимизации могут быть весьма разнообразными. Чтобы ориентироваться в этом многообразии, введем некоторую классификацию (рис. 1).

Рисунок 1

Любой объект может характеризоваться совокупностью параметров. Движение к оптимуму возможно, если выбран один единственный параметр оптимизации. Тогда прочие характеристики процесса уже не выступают в качестве параметров оптимизации, а служат ограниче­ниями. Другой путь – построение обобщенного параметра оптимизации как некоторой функции от множества исходных.

Требования к параметру оптимизации

Параметр оптимизации – это признак, по которому оптимизируется процесс. Он должен быть количественным, задаваться числом. Множество значений, кото­рые может принимать параметр оптимизации, на­зывается областью его определения. Области определения могут быть непрерывными и дискретными, ограниченны­ми и неограниченными.

Измерять параметр оптимизации - это значит располагать подходящий прибором. Если нет способа количественного измерения резуль­тата, то приходится воспользоваться приемом, называе­мым ранжированием (ранговым подходом). При этом пара­метрам оптимизации присваиваются оценки – ранги по заранее выбранной шкале: двухбалльной, пятибалльной и т.п. Ранговый параметр имеет дискретную ограниченную область определения. В простейшем случае область содержит два значения (да, нет; хорошо, плохо). Это может соответствовать, например, годной продукции и браку.

Ранг – это количественная оценка параметра оптимизации, но она носит условный (субъективный) характер.

Для каждого физически измеряемого параметра опти­мизации можно построить ранговый аналог. Потребность в построении такого аналога возникает, если имеющиеся в распоряжении исследователя численные характеристи­ки неточны или неизвестен способ построения удовлет­ворительных численных оценок. При прочих равных ус­ловиях всегда нужно отдавать предпочтение физическому измерению, так как ранговый подход менее чувствителен и с его помощью трудно изучать тонкие эффекты.

Следующее требование: параметр оптимизации должен выражаться одним числом. Иногда это получается как регистрация показания прибора. Например, скорость движения машины определяется чис­лом на спидометре.

Еще одно требований, связанное с количественной при­родой параметра оптимизации, – однозначность в статистическом смысле. Заданному набору значений фак­торов должно соответствовать одно с точностью до ошибки эксперимента значение параметра оптимизации. Однако обратное неверно: одному и тому же значении параметра могут соответствовать разные наборы значений факторов.

Существует требование, при котором параметр определяется с наибольшей возможной точностью. (Если и эта точность недостаточна, тогда приходится обращаться к увеличению числа повторных опытов.)

Следующее требование к параметру оптимизации – требование универсальности или полноты. Под универсальностью параметра оптимизации понимает­ся его способность всесторонне характеризовать объект. В частности, технологические параметры оптимизации не­достаточно универсальны: они не учитывают экономи­ку. Универсальностью обладают, например, обобщенные параметры оптимизации, Которые строятся как функции от нескольких частных параметров.

Желательно, чтобы параметр оптимизации имел физический смысл, был простым и легко вычисляемым.

Требование физического смысла связано с последу­ющей интерпретацией результатов эксперимента. Не пред­

Дата добавления: 2015-08-20