Бергер предложил разделимые коды, обнаруживающие все ошибки в идеальном асимметричном канале [2]. В каждой кодовой комбинации длины n m элементов являются проверочными. Проверочные элементы формируются по следующему принципу: подсчитывается число единиц в информационных разрядах и записывается в виде m разрядного двоичного числа, которое инвертируется, и полученный результат приписывается в качестве избыточности к кодовой комбинации простого кода.
Таким образом, m равно наименьшему целому числу, превышающему 
, т.е. 
. Коды Бергера, образованные подобным образом, обозначают 
Например, рассмотрим процесс формирования комбинации кода Бергера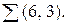 
для комбинации простого кода 011010. Число 1 в этой комбинации равно 3 – в двоичной записи 011. Инвертированное число (100) и приписывается в качестве проверочных элементов к комбинации простого кода: 100011010. Это и есть искомая комбинация.
Коды Бергера обнаруживают все ошибки в асимметричных каналах, т.к. асимметричная ошибка по разному влияет на информационные и проверочные символы кодовой комбинации, благодаря инвертированию последних.
Дата добавления: 2015-08-02; просмотров: 167 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Коды с постоянным весом | | | Принципы построения каскадных кодов |