Наиболее известные сверточные коды

Векторы связи или порождающие многочлены сверточного кода обычно выби­раются исходя из свойств просветов кода. Главным критерием при выборе кода является требование, чтоб код не допускал катастрофического распространения ошибок и имел максимальный просвет при данной степени кодирования и длине кодового ограничения.

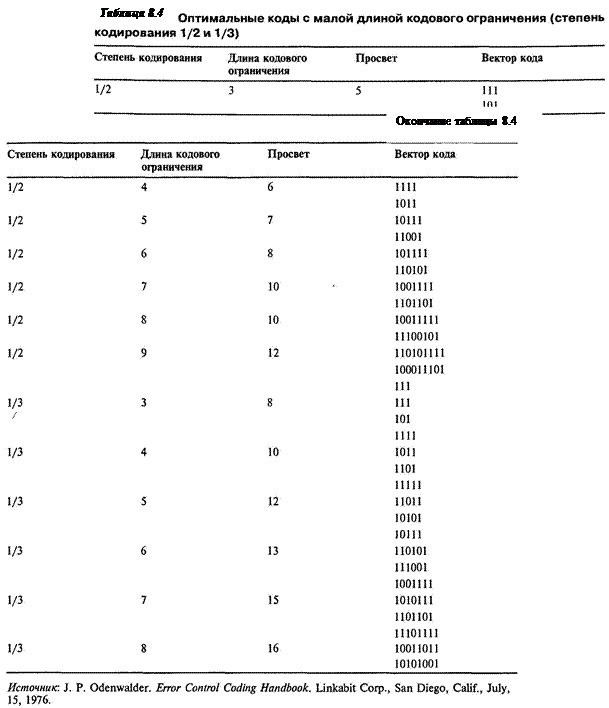
Затем при данном просвете d_f минимизируется число путей или число ошибочных би­тов данных, которые представляют путь. Процедуру выбора можно усовершенство­вать, рассматривая количество путей или ошибочных битов при d_f+1, d_f + 2 и т.д., пока не останется только один код или класс кодов. Список наиболее известных ко­дов со степенью кодирования 1/2 при К, равном от 3 до 9, и со степенью кодирования 1/3 при К, равном от 3 до 8, соответствующих этому критерию, был составлен Оденуальдером (Odenwalder) и приводится в табл. 8.4. Векторы связи в этой таблице представляют наличие или отсутствие (1 или 0) соединения между соответствующими регистрами сверточного кодера, причем крайний левый элемент соответствует край­нему левому разряду регистра кодера. Интересно, что эти соединения можно обратить (заменить в указанной выше схеме крайние левые на крайние правые). При декоди­ровании по алгоритму Витерби обратные соединения приведут к кодам с точно таки­ми же пространственными характеристиками, а значит, и с такими же рабочими ха­рактеристиками, как показаны в табл. 8.4.

Задачи

1. Для передачи речи в сетях мобильной связи GSM используется оптимальный сверточный код с порождающими многочленами g₁(x) =1+х³+х⁴ и g₂(x) =1+х+х³+х⁴, имеющий свободное расстояние, равное d_free= 7 [7]. Построить схему кодера и определить число его состояний. Сколько метрик должен вычислять декодер на каждом шаге декодирования? Сколько выживших путей выбирается для продолжения декодирования?

2. Для передачи данных в сети GSM используется сверточный код с порождающими многочленами g₁(x) =1+х³+х⁴, g₂(x) =1+х+х³+х⁴, g₁(x) =1+х²+х⁴ и g₃(x) =1+ х+х²+х³+х⁴, имеющий свободное расстояние, равное d_free= 12 [7]. Построить схему кодера и определить число его состояний. Сколько метрик должен вычислять декодер на каждом шаге декодирования? Сколько выживших путей выбирается для продолжения декодирования?

3. Наиболее широко используемый до настоящего времени сверточный код это, так называемый стандартный код НАСА США [3]. Он характеризуется следующими данными: k/n=1/2, К=7, d_free =10, вектора связи:1001111 и 1101101. Построить схему кодера и определить число его состояний.

4. Построить порождающую матрицу для каждого кода из трех предыдущих задач.

Дата добавления: 2015-08-02