Распределение весов

В этом разделе рассматривается метод определения спектра ве­сов линейного блокового кода, построенного из сверточного кода скорости 1/n с помощью рассмотренных выше конструк­ций [WV], Обозначим Ω(x) переходную матрицу состояний ко­дера размера 2^т х 2^т и вида:

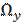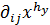(x) = (2.1)

где 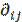=1, если и только если имеется переход из состояния i в состояние j. В противном случае 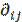= 0. Величина 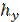равна Хеммингову весу соответствующего выходного вектора (длины п).

Пример 4. Для сверточного кодера переходная матрица состояний Ω(x) равна

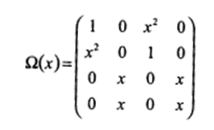
Распределение весов двоичного линейного блокового (n, к) ко­да, построенного любым из рассмотренных выше способов, может быть получено просто возведением данной переходной матрицы в l-ую степень, обозначенную 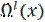и комбинирова­нием различных членов.

Каждый элемент 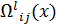переходной матрицы дает распре­деление весов путей на решетке, которые начинаются в состо­янии i и заканчиваются в состоянии j через l шагов (тактов ввода). Для конструкции ZT (нулевой хвост) значение = к + т, тогда как для конструкций DT и ТВ l = k. Распределение весов для каждой из рассмотренных выше конструкций было полу­чено следующим способом.

Терминированная конструкция (ZT):

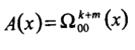(2.2)

Усеченная конструкция (DT):

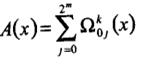(2.3)

Кольцевая конструкция (ТВ):

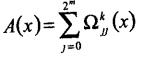(2.4)

Пример 5. Рассмотрим снова сверточный кодер памяти 2 и скорости 1/2. Для него находим:

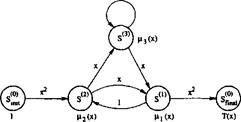
Рис. 2.1. Модифицированная диаграмма состояний кодера памяти 2 и скорости ½.

Распределение весов усеченной конструкции из Примера 4 получается суммированием членов первой строки полученной выше матрицы.[3].

Дата добавления: 2015-08-02