Модель канала с АБГШ

Пожалуй, наиболее важной моделью для систем цифровой связи является модель канала с аддитивным белым гауссовым шумом (АБГШ - additive white Gaussian noise (AWGN)). В этом разделе выводятся оценки вероятности ошибки декодирова­ния и вероятности ошибки на бит для линейных кодов в кана­ле с АБГШ. Хотя аналогичные выражения оказываются спра­ведливыми и для сверточных кодов, они будут выведены в по­следующих разделах, вместе с обсуждением декодирования с «мягким решением» по алгоритму Витерби. Следующие ни­же результаты содержат необходимые инструменты для оцен­ки помехоустойчивости двоичных систем кодирования в гаус­совом канале.

Рассмотрим двоичную систему передачи сигналов, в кото­рой кодовые символы {0,1} отображаются в действительные числа {+1,-1}, соответственно, как показано на Рисунке 8. В дальнейшем, вектора имеют размерность и и обозначение v = (хд, v_n_i). Условная функция плотности вероятности (ф.п.в.) последовательности r на выходе канала при условии, что на его входе передавалась последовательность v, равна

(1.1)

где р„(п) есть ф.п.в. и статистически независимых и одинаково распределенных (i.i.d.) отсчетов шума, каждый из которых имеет Гауссово распределение с нулевым средним и дисперси­ей, раной jVo/2. Величина Nq называется односторонней спек­тральной плотностью мощности шума. Легко показать, что де­кодирование по максимуму правдоподобия (м.п.) линейного кода в таком канале соответствует выбору последовательности v', минимизирующей квадрат Евклидова расстояния между при­нятой последовательностью r и v', т.е.

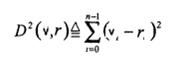
(1.2)

Следует заметить, что декодер, использу­ющий (1.2) как метрику, называется декодером с мягким реше­нием не зависимо от того, используется или нет принцип мак­симума правдоподобия.

Рис.1.1. Система двоичной передачи с кодированием по каналу с АБГШ.

В этой главе рассматривается декодирование с (дополнитель­ной) «мягкой» информацией, получаемой из канала. Рассмотрим простой случай передачи двоичных сигналов по каналу с АБГШ (аддитивным белым гауссовым шумом). Чтобы обосновать це­лесообразность применения декодирования с мягким решени­ем заметим, что шумовая компонента в задаче восстановления данных или приема сигналов является непрерывной, т.е. не дис­кретной, по своей природе. Это означает, что принятые симво­лы представляются (квантованными) действительными числами (соответствующими напряжению, току и т.п.), а не двоичными символами или символами из конечного поля GF(2^m).

Когда выбираются жесткие решения относительно приня­тых символов, при посимвольной обработке, то могут проис­ходить ошибки. Это иллюстрируется на рис. 1.2.

В принципе существуют два метода декодирования поме­хоустойчивых кодов, основанных на принятой последователь­ности действительных чисел:

1. Декодирование с жестким решением (hard decision decoding) (HDD): при формировании жестких решений относительно принятых из канала величин происходят ошибки. Цель HDD состоит в исправлении двоичных ошибок, возникших в процессе вы­бора жестких решений. Первая часть этой книги была посвя­щена описанию различных методов HDD для линейных бло­ковых кодов, циклических и сверточных кодов.

Рис. 1.2. Пример возникновения ошибок при декодировании с жестким решением

2. Декодирование с мягким решением (soft-decision decoding) (SDD):

принятые из канала величины вводятся непосредственно в де­кодер для формирования оценок кодовой последовательности. Особым случаем SDD является декодирование по максимуму правдоподобия (maximum-likelihood decoding) (MLD или МПД), при котором в качестве решения декодера выбирается ближайшая (в некоторой метрике) кодовая последователь­ность. Здесь важно помнить, что для SDD необходимо знать статистику шума в канале связи.

В общем случае SDD более трудоемко, чем HDD. Отметим две основных причины этого. Одна из них состоит в том, что SDD требует выполнения операций с действительными числа­ми. В практических применениях эти числа квантуются с ко­нечной точностью (т.е. представляются конечным числом бит). Для некоторых систем передачи двоичных сигналов изве­стно, что квантование на 8 уровней (или трех-битное представ­ление чисел) обеспечивает эффективность системы, близкую к использованию вычислений с бесконечной точностью (без квантования) [2].

Другая причина увеличения сложности SDD связана с не­обходимостью вычисления апостериорных статистик для ко­довых символов. Тем не менее, увеличение трудоемкости оку­пается потенциальным повышением эффективности системы кодирования. Как показано в Главе 1 для двоичных сигналов в Гауссовом канале в случае SDD та же самая эффективность достигается при отношении сигнал-шум на 2 — 3 dB меньше, чем при HDD. Это означает, что в случае SDD излучаемая пе­редатчиком мощность может быть снижена на 50 — 63% по сравнению со случаем HDD. Эта экономия мощности преоб­разуется в

меньший размер передающей антенны или в меньший размер приемной антенны при той же мощности пере­датчика.

Дата добавления: 2015-08-02