Пространственные характеристики сверточных кодов

Рассмотрим пространственные характеристики сверточных кодов в контексте простого кодера (рис. 8.3) и его решетчатой диаграммы (рис. 8.7). Мы хотим узнать расстояния между всеми возможными парами последовательностей кодовых слов. Как и в случае блочных кодов, нас интересует минимальное расстояние между всеми такими парами последовательностей кодовых слов в коде, поскольку минимальное расстояние связано с возможностями коррекции ошибок кода. Поскольку сверточный код является групповым или линейным, можно без потери общности просто найти минимальное расстояние между последовательностью кодовых слов и нулевой после­довательностью. Другими словами, для линейного кода данное контрольное сообще­ние окажется точно таким же "хорошим", как и любое другое. Так почему бы не взять то сообщение, которое легко проследить, а именно нулевую последователь­ность? Допустим, что на вход передана нулевая последовательность; следовательно, нас интересует такой путь, который начинается и заканчивается в состоянии 00 и не возвращается к состоянию 00 нигде внутри пути. Всякий раз, когда расстояние любых других путей, которые сливаются с состоянием а = 00 в момент t_i, окажется меньше расстояния нулевого пути, вплоть до момента t_i, будет появляться ошибка, вызывая в процессе декодирования отбрасывание нулевого пути. Иными словами, при нулевой передаче ошибка возникает всегда, когда не выживает нулевой путь. Следовательно, ошибка, о которой идет речь, связана с выживающим путем, который расходится, а затем снова сливается с нулевым путем. Может возникнуть вопрос, зачем нужно, что­бы пути сливались? Не будет ли для обнаружения ошибки достаточно лишь того, что­бы пути расходились? В принципе, достаточно, но если ошибка характеризуется толь­ко расхождением, то декодер, начиная с этой точки, будет выдавать вместо оставшего­ся сообщения сплошной "мусор". Мы хотим выразить возможности декодера через число обычно появляющихся ошибок, т.е. хотим узнать "самый легкий" для декодера способ сделать ошибку. Минимальное расстояние для такой ошибки можно найти, полностью изучив все пути из состояния 00 в состояние 00. Итак, давайте сначала за­ново начертим решетчатую диаграмму, как показано на рис. 8.14, и обозначим каж­дую ветвь не символом кодового слова, а ее расстоянием Хэмминга от нулевого кодо­вого слова. Расстояние Хэмминга между двумя последовательностями разной длины можно получить путем их сравнивания, т.е. прибавив к началу более короткой после­довательности нужное количество нулей. Рассмотрим все пути, которые расходятся из нулевого пути и затем в какой-то момент снова сливаются в произвольном узле. Из диаграммы на рис. 8.14 можно получить расстояние этих путей до нулевого пути. Итак, на расстоянии 5 от нулевого пути имеется один путь; этот путь отходит от нуле­вого в момент t₁ и сливается с ним в момент t₄.. Точно так же имеется два пути с рас­стоянием 6, один отходит в момент t₁ и сливается в момент t₅ а другой отходит в мо­мент t₁ и сливается в момент t₆ и т.д. Также можно видеть (по пунктирным и сплош­ным линиям на диаграмме), что входными битами для расстояния 5 будут 1 0 0; от

нулевой входной последовательности эта последовательность отличается только одним битом. Точно так же входные биты для путей с расстоянием 6 будут 1 1 0 0 и 1 0 1 0 0; каждая из этих последовательностей отличается от нулевого пути в двух местах. Ми­нимальная длина пути из числа расходящихся, а затем сливающихся путей называется минимальным просветом (minimum free distance), просветом или свободным расстоянием (free distance). Его можно видеть на рис. 8.14, где он показан жирной линией. Оценка возмож­ностей кода по коррекции t ошибок, определяется известным уравнением с заменой минимального расстояния d_min на просвет (свободное расстояние) d_f

Здесь [x] означает наибольшее целое, не большее х. Положив d_f = 5, можно видеть, что код, описываемый кодером на рис. 8.3, может исправить две любые ошибки канала.

Решетчатая диаграмма представляет собой "правила игры". Она является как бы символическим описанием всех возможных переходов и соответствующих начальных и конечных состояний, ассоциируемых с конкретным конечным автоматом. Эта диа­грамма позволяет взглянуть глубже на выгоды (эффективность кодирования), которые дает применение кодирования с коррекцией ошибок. Взглянем на рис. 8.14 и на воз­можные ошибочные расхождения и слияния путей. Из рисунка видно, что декодер не может сделать ошибку произвольным образом. Ошибочный путь должен следовать од­ному из возможных переходов. Решетка позволяет нам определить все такие доступ­ные пути. Получив по этому пути кодированные данные, мы можем наложить огра­ничения на переданный сигнал. Если декодер знает об этих ограничениях, то это по­зволяет ему более просто (используя меньшее значение сигнал/помеха - E_b/N₀) удовлетворять требованиям надежной безошибочной работы.

Хотя на рис. 8.14 представлен способ прямого вычисления просвета, для него можно получить более строгое аналитическое выражение, воспользовавшись для этого диаграммой состояний, изображенной на рис. 8.5. Для начала обозначим ветви диа­граммы состояний как D⁰= 1, D¹ или D², как это показано на рис. 8.15, где показатель D означает расстояние Хэмминга между кодовым словом этой ветви и нулевой вет­вью. Петлю в узле а можно убрать, поскольку она не дает никакого вклада в про­странственные характеристики последовательности кодовых слов относительно нуле­вой последовательности. Более того, узел а можно разбить на два узла (обозначим их а и е), один из них представляет вход, а другой — выход диаграммы состояний. Все пути, начинающиеся из состояния а = 00 и заканчивающиеся в е = 00, можно просле­дить на модифицированной диаграмме состояний, показанной на рис. 8.15. Переда­точную функцию пути a b c e (который начинается и заканчивается в состоянии 00) можно рассчитать через неопределенный "заполнитель" D как D²DD² = D⁵. Степень D — общее число единиц на пути, а значит, расстояние Хэмминга до нулевого пути. Точно так же пути a b d

c e и a b c b e e имеют передаточную функцию D⁶ и, соответст­венно, расстояние Хэмминга, равное 6, до нулевого пути. Теперь уравнения состоя­ния можем записать следующим образом:

X_b = D²X_a+X_c,

X_c = DX_b+DX_d,

X_d = DX_b+DX_d,

X_e = D²X_c.

Здесь Х_a,..., Х_е являются фиктивными переменными неполных путей между промежу­точными узлами. Передаточную функцию кода, T(D), которую иногда называют произ­водящей функцией кода, можно записать как T(D) = X_e/X_a. Решение уравнений состоя­ния имеет следующий вид:

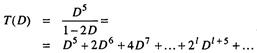
Передаточная функция этого кода показывает, что имеется один путь с расстоянием 5 до нулевого вектора, два пути — с расстоянием 6, четыре — с расстоянием 7. В общем случае существуют 2 ^l пути с расстоянием l + 5 до нулевого вектора, причем l = 0, 1, 2,.... Просвет d_f кода является весовым коэффициентом Хэмминга слагаемого, имеющего наименьший порядок в разложении T(D). В данном случае d_f = 5. Для оценки пространственных характеристик при большой длине кодового ограничения передаточную функцию T(D) использовать нельзя, поскольку сложность T(D) экспо­ненциально растет с увеличением длины кодового ограничения.

С помощью передаточной функции кода можно получить более подробную ин­формацию, чем при использовании лишь расстояния между различными путями. В каждую ветвь диаграммы состояний введем множитель L так, чтобы показатель L мог служить счетчиком ветвей в любом пути из состояния а = 00 в состояние е = 00.

Более того, мы можем ввести множитель N во все ветви переходов, порожденных входной двоичной единицей. Таким образом, после прохождения ветви суммарный множитель N возрастает на единицу, только если этот переход ветви вызван входной битовой единицей. Для сверточного кода, описанного на рис. 8.3, на перестроенной диаграмме состояний (рис. 8.16) показаны дополнительные множители L и N. Уравне­ния теперь можно переписать следующим образом:

X_b = D²LNX_a+LNX_c,

X_c = DLX_b+DLX_d,

X_d = DLNX_b+DLNX_d,

X_e = D²LX_c.

Передаточная функция кода такой доработанной диаграммы состояний будет следующей:

Таким образом, мы можем проверить некоторые свойства путей, показанные на рис. 8.14. Существует один путь с расстоянием 5 и длиной 3, который отличается от нулевого пути одним входным битом. Имеется два пути с расстоянием 6, один из них имеет длину 4, другой — длину 5, и оба отличаются от нулевого пути двумя входными битами. Также есть пути с расстоянием 7, из которых один имеет длину 5, два — дли­ну 6 и один — длину 7; все четыре пути соответствуют входной последовательности, которая отличается от нулевого пути тремя входными битами. Следовательно, если нулевой путь является правильным и шум приводит к тому, что мы выбираем один из неправильных путей с расстоянием 7, то в итоге получится три битовые ошибки.

Дата добавления: 2015-08-02