|
Читайте также: |
Пусть известно значение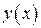 
и требуется вычислить значение 
. Рассмотрим равенство:
. (2.3)
Как было показано в главе 1, при замене интеграла в правой части на 
погрешность имеет порядок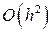 
. Таким образом,
.
Поскольку 
, то мы получаем
.
Отбрасывая член порядка 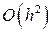, и обозначая 
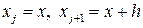, получаем формулу Эйлера:
.
Дата добавления: 2015-08-02; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ | | | Различные модификации метода Эйлера |