Читайте также:
|
Для получения более точной формулы нужно точнее аппроксимировать интеграл в правой части.
Воспользуемся квадратурной формулой трапеции, получим
,
или иначе,
.
Заменим 
в правой части полученной формулы на некоторую величину 
. Тогда правая часть изменится на величину
(
находится между 
и ). Таким образом, имеет место соотношение
.
Условию удовлетворяет результат вычислений по формуле Эйлера 
. Эти соотношения определяют пару расчетных формул:
(2.4)
Рассмотренный метод носит название метода Эйлера-Коши.
Построим другую пару формул с погрешностью на шаге того же порядка. Интеграл в правой части (2.3) заменим по формуле средних прямоугольников:
,
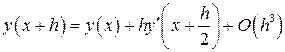или
.
Если 
, то, как и в предыдущем случае, имеем
.
В качестве можно взять результат вычислений по формуле Эйлера с шагом 
: 
. Этим соотношениям соответствуют пара расчетных формул, определяющих еще одну модификацию метода Эйлера:
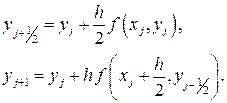(2.5)
Дата добавления: 2015-08-02; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Эйлера | | | Оценка погрешности по правилу Рунге |