Численные методы решения задачи Коши для обыкновенного дифференциального уравнения

Задача Коши для обыкновенного дифференциального уравнения первого порядка состоит в отыскании решения уравнения

, (2.1)

удовлетворяющего начальному условию

(2.2)

Разобьем отрезок , на котором ищем решение, на равных интервалов с шагом 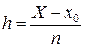. Получим следующие точки деления: . При решении задачи Коши численным методом для любого 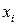определим приближенно , 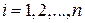. Величина погрешности этих значений, т.е. разность между точным решением и приближенным в соответствующих точках, определяет погрешность метода. В данной главе мы рассмотрим различные методы численного решения задачи Коши.

Дата добавления: 2015-08-02