Кодирование укрупненных блоков

Размер блока	Кодируемые блоки	Вероят-ности	Кодовые группы	Число знаков в группе	Среднее число знаков в группе	Среднее число знаков на букву
Две буквы	х 1 х 1	0,81			1,29
х 1 х 2	0,09
х 2 х 1 х 2 х 2	0,09 0,01
Три буквы	х 1 х 1 х 1 х 1 х 1 х 2 х 1 х 2 х 1 х 2 х 1 х 1	0,729 0,081 0,081 0,081			1,698
х 1 х 2 х 2	0,009
х 2 х 1 х 2 х 2 х 2 х 1 х 2 х 2 х 2	0,009 0,009 0,001

При кодировании укрупненных блоков уменьшается также избыточность, обусловленная статистическими связями между элементами сообщений. Это объясняется тем, что укрупнение алфавита источника приводит к декорреляции сообщений: вероятностные связи между блоками слабее, чем между отдельными элементами, и чем длиннее блоки, тем меньше зависимость между ними.

Пропускная способность дискретного канала с шумами. Из соотношения (6-285), определяющего пропускную способность дискретного канала в общем случае, могут быть получены формулы для конкретных каналов. Приводимые ниже формулы справедливы для дискретных каналов без памяти (см. § 6-11), в которых используются символы одинаковой длительности τ и отсутствуют какие-либо запреты на допустимую последовательность передачи символов. Для таких каналов скорость передачи символов кода .

1. Однородный симметричный канал. Его пропускная способность

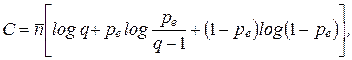(6-295)

где

при i ≠ j.

В случае двоичного канала

(6-296)

Из выражения (6-295) следует, что С = 0 при р_е = (q - 1)/ q. На рис. 6-62 приводится зависимость пропускной способности двоичного симметричного канала от вероятности ошибки р_е. Как видно из графика, при р_е = 0,5 пропускная способность С = 0. Это объясняется следующим. При вероятности ошибок р_е = 0,5 принимаемая последовательность не содержит никакой информации о передаваемой последовательности. В этих условиях можно было бы не передавать никаких сигналов, а принимать решение на приемной стороне, например по результатам бросания монеты (цифра или герб).

Рис. 6-62. Зависимость пропусков способности двоичного канала

от вероятности ошибки.

При р_е > 0,5 с увеличением вероятности ошибок, пропускная способность возрастает. Это обусловлено тем, что при р_е ≠ 0,5 неопределенность ситуации уменьшается и при р_е > 0,5 имеется возможность извлечь из принимаемого сигнала больше информации. Для этого надо изменить правило распознавания сигналов на обратное, т.е. считать, что принятая 1 соответствует переданному 0, и наоборот. При этом вероятность ошибочного приема станет равной (1 - р_е) < 0,5.

2. Однородный несимметричный канал. Максимальная скорость передачи в несимметричных каналах достигается не при равных вероятностях символов, а при некотором неравновероятном распределении, когда чаще используются символы, имеющие большую вероятность правильного приема.

В качестве примера рассмотрим двоичный канал, в котором символ 1 всегда принимается верно (крайняя несимметрия), т.е.

Пропускная способность такого канала определяется выражением

(6-297)

где

С увеличением р_е от 0 до 1 пропускная способность канала падает от до 0. Можно показать, что при р_е = 0,5 пропускная способность равна С = 0,322 и достигается она при априорных вероятностях

р _опт (0) = 0,4; р _опт (1) = 0,6.

3. Однородный симметричный стирающий канал. Его пропускная способность

(6-298)

где р_с - вероятность стирания символа.

Если канал является двоичным, то

(6-299)

В тех случаях, когда можно пренебречь вероятностью ошибочного приема по сравнению с вероятностью стирания, пропускная способность рассчитывается по более простой формуле

С ≈ (1 - р_с) log q. (6-300)

Дата добавления: 2015-08-02