Характеристики непрерывных каналов связи

Скорость передачи и пропускная способность. Общие выражения, определяющие скорость передачи и пропускную способность непрерывных каналов (рис. 6-59), имеют такой же вид, как и в случае дискретных каналов (6-285), (6-286), с той лишь разницей, что вместо энтропии множества символов здесь используются дифференциальные энтропии h_T (S) и h_T (S | S *) множества реализаций сигналов S на некотором интервале длительностью Т.

В соответствии с этим

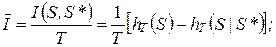(6-302)

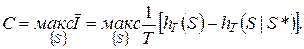(6-303)

При фиксированных характеристиках канала связи со структурной схемой на рис. 6-59 максимум в (6-303) отыскивается по всем возможным множествам (способам формирования) входных (модулирующих) сигналов { S }. Если способ модуляции и демодуляции радиосигналов не определен, то максимум может также отыскиваться и по всем возможным способам модуляции и демодуляции. В таком случае значение С может истолковываться как пропускная способность линейного тракта 2, рассматриваемого как канал, отыскиваемая по всем возможным множествам (способам формирования) радиосигналов { S_p }.

Таким образом, пропускная способность непрерывного канала (так же как и дискретного) зависит только от свойств канала, которые определяются шумами и ограничениями, накладываемыми на канал. Естественно, что пропускная способность зависит от состава устройств, образующих канал. Например, пропускная способность канала на рис. 6-59, при фиксированных (неоптимальных) способах модуляции и демодуляции, будет меньше пропускной способности его линейных трактов.

Если принимаемый сигнал S *(t) является суммой независимых сигнала S (t) и шума N (t), то вместо (6-302) можно записать:

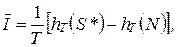(6-304)

где h_T (N) - дифференциальная энтропия шума.

На основе этого выражения получены формулы для расчета пропускной способности непрерывных каналов с учетом накладываемых ограничений. К последним обычно относятся такие характеристики, как средняя или максимальная мощность полезного сигнала и спектральная плотность мощности шума.

Далее рассматриваются примеры определения пропускной способности некоторых типов каналов с ограниченной полосой пропускания Δ f и стационарным шумом, статистически независимым от полезного сигнала. Во всех случаях, кроме формул (6-309), (6-310), шум является гауссовым. Отметим, что приводимые в этом параграфе результаты непосредственно относятся к линейным трактам 1 и 2 в структурной схеме на рис. 6-59. Оценка влияния способа модуляции на пропускную способность дается в § 6-13.

Каналы с ограниченной средней мощностью сигнала. Если в канале с полосой пропускания Δ f действует стационарный гауссовский шум, статистически независимый от полезного сигнала, то в (6-304) h_T (N) не зависит от выбора { S } и скорость передачи информации 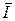будет максимальна, если h_T (S *) = макс. Последнее условие выполняется, если полезный сигнал S (t) также будет гауссовским процессом. При этом скорость передачи информации [13, 18]

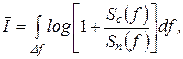(6-305)

где S_c (f), S_п (f)- спектральные плотности сигнала и помех (шума) на входе приемного устройства. Соотношение (6-305) позволяет решать разнообразные задачи об отыскании оптимальных спектров сигнала или шума при различных ограничениях, накладываемых на параметры канала.

Если заданы средняя мощность сигнала Р_с и спектральная плотность мощности шума S_п (f) на входе приемного устройства, то скорость передачи будет зависеть только от распределения мощности полезного сигнала по частоте, т.е. от вида функции S_п (f). Максимальная скорость передачи (пропускная способность) достигается при выполнении условия

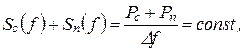(6-306)

где

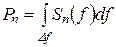
- средняя мощность шума.

При этом

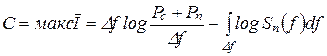(6-307а)

Физический смысл условия (6-306) поясняется с помощью рис. 6-64, на котором изображены примерные графики спектральных плотностей сигнала и помехи. Для достижения максимальной скорости передачи информации спектральная плотность сигнала (на рисунке заштрихована) должна быть такой, чтобы основная часть мощности сигнала была сосредоточена в той области спектра, где мала спектральная плотность помехи.

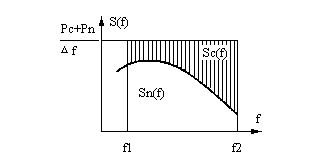
Рис. 6-64. К определению спектральной плотности мощности сигнала, обеспечивающей максимальную скорость передачи.

Анализ (6-307а) позволяет установить, что при фиксированных значениях средних мощностей сигнала и шума наименьшую пропускную способность имеет канал, в котором действует гауссовский шум с постоянной спектральной плотностью N ₀ в полосе Δ f канала. Такая помеха образуется при действии на входе приемника белого гауссовского шума. Из этого следует, что белый гауссовский шум обладает наибольшим мешающим действием.

Подставляя в (6-307а) значение 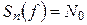и учитывая, что 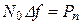, получаем известную формулу Шеннона для канала с белым гауссовским шумом (такой канал обычно называют гауссовым):

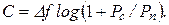(6-307б)

Для достижения максимальной скорости передачи, определяемой (6-307б), полезный сигнал в соответствии с условием (6-306) должен обладать постоянной спектральной плотностью S ₀, т.е. быть шумоподобным. Так как обычно это условие не выполняется, то скорость передачи в реально существующих каналах значительно ниже их пропускной способности. Таким образом, (6-307б) определяет верхний предел скорости передачи информации в гауссовом канале.

Из (6-307б) видно, что при фиксированном отношении Р_с / Р_п пропускная способность прямо пропорциональна полосе частот. Следует, однако, иметь в виду, что в реальных каналах с увеличением полосы пропускания растет и мощность шума. Поэтому представляет интерес зависимость пропускной способности канала от полосы частот при фиксированном значении отношения P_c / N ₀, которое не зависит от полосы частот. Если сигнал занимает полосу частот Δ f, то в этом случае

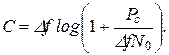(6-307б)

Анализ этой зависимости показывает, что с увеличением полосы пропускная способность канала растет не безгранично, а стремится к пределу

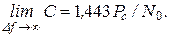(6-308)

Последнее соотношение означает, что при малом отношении сигнал / шум 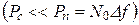пропускная способность канала не зависит от ширины полосы пропускания, а определяется лишь отношением средней мощности полезного сигнала к спектральной плотности шума. Это положение хорошо согласуется с выводами теории идеального приема (см. разд. 7).

Для каналов с произвольным шумом Шенноном найдены верхняя и нижняя границы пропускной способности

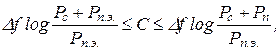(6-309)

где Р _п.э. - энтропийная мощность шума (см. § 6-10).

При значениях Р_с ≥ Р_п обе границы сближаются и можно пользоваться приближенной формулой

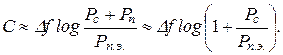(6-310)

Так как всегда Р_п.э. ≤ Р_п, то пропускная способность канала с произвольным шумом при фиксированных значениях Δ f, Р_с и Р_п больше пропускной способности канала с белым гауссовским шумом.

Каналы с ограниченной пиковой (максимальной) мощностью. Для таких каналов найдены лишь границы пропускной способности в условиях белого гауссовского шума

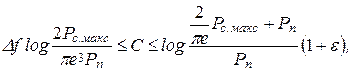(6-311)

где Р_с.макс - допустимая пиковая (максимальная) мощность сигнала; ε → 0 при Р_с.макс / Р_п → ∞.

При этом нижняя граница справедлива для любых значений Р_с.макс / Р_п, а верхняя - только для Р_с.макс / Р_п >> 1.

Для малых значений Р_с.макс / Р_п при условии, что полоса канала начинается от нуля, справедлива приближенная формула

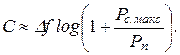(6-312)

Каналы с переменными параметрами. Рассмотрим канал со случайным коэффициентом передачи К с заданной одномерной плотностью вероятности p (k) (канал с замираниями). Предположим, что коэффициент k изменяется настолько медленно, что имеется возможность на основе анализа ранее принятых сигналов с большой точностью предсказывать значение k в рассматриваемый момент времени (случай медленных замираний). В этих условиях для пропускной способности канала с белым гауссовским шумом справедлива приближенная формула

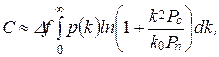нт/с,

где k ₀ - среднее квадратическое значение коэффициента К.

Наиболее распространенным является случай релеевских замираний, когда

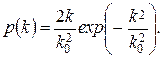
При этом

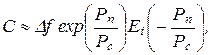(6-313)

где

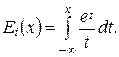
Из (6-313) следует:

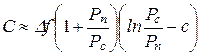при Р_с >> Р_п; (6-314)

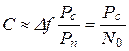при Р_с << Р_п, (6-315)

где с ≈ 0,5772 - постоянная Эйлера.

Анализ выражения (6-313) показывает, что медленные релеевские замирания понижают пропускную способность канала не более чем на 17 %.

Теорема Шеннона для непрерывных каналов. Если поток информации источника непрерывных сообщений 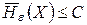, то существует метод передачи, при котором все сообщения источника могут быть переданы по данному каналу и воспроизведены на его выходе с точностью, сколь угодно близкой к ε. Это невозможно, если .

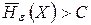Сформулированная теорема позволяет находить предельно достижимую эффективность непрерывных каналов и с этой точки зрения оценивать методы передачи, используемые в реальных каналах (см. § 6-13).

Всякий дискретный канал (рис. 6-60) имеет в своем составе непрерывный канал. Можно считать, что дискретный канал получается из непрерывного путем наложения на последний некоторых дополнительных ограничений (например, задано основание кода, определен вид используемых сигналов, выбран алгоритм работы решающего устройства). Все это приводит к тому, что пропускная способность дискретного канала не может быть больше пропускной способности входящего в его состав непрерывного канала.

Это хорошо видно при сравнении пропускных способностей непрерывного гауссовского канала (6-307) и построенного на его основе двоичного симметричного канала (6-296). Принимая для этого канала 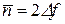, что является верхним пределом скорости передачи двоичных символов, получаем:

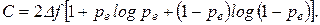
Вероятность неправильного приема символов р_е зависит от отношения сигнал / шум в канале, стремясь к нулю при увеличении Р_с / Р_п. При этом С → 2Δ f. Следовательно, в то время как пропускная способность непрерывного канала с ростом Р_с / Р_п увеличивается неограниченно (это видно из (6-307), пропускная способность двоичного дискретного канала ограничена величиной 2Δ f. Это обусловлено тем, что двоичные сигналы значительно отличаются от белого гауссовского шума. Распределение вероятностей текущего значения этих сигналов отлично от нормального, ибо в алфавите используются лишь два разных символа и не выполняется условие, при котором реализуется пропускная способность гауссовского канала. Аналогичная картина наблюдается и при рассмотрении других типов дискретных каналов [14].

Из сказанного не следует, однако, делать вывод о преимуществах непрерывных (аналоговых) методов передачи информации по сравнению с дискретными (цифровыми). Здесь речь шла лишь о предельных теоретических возможностях, практическая реализация которых для непрерывных и дискретных каналов различна.

Дата добавления: 2015-08-02