
Читайте также:
|
Общие сведения. К основным информационным характеристикам канала относятся скорость передачи информации и пропускная способность канала.
С к о р о с т ь п е р е д а ч и и н ф о р м а ц и и определяется средним количеством информации, передаваемым по каналу в единицу времени:
 (6-285)
(6-285)
где < τ > - средняя длительность символов используемого алфавита сигналов; H (A) и Н (A | A *) - априорная и апостериорная энтропии, приходящиеся на один символ.
Минимально допустимое значение < τ > в канале связи зависит от полосы частот Δ f, предоставляемой сигналам этого канала. Энтропия Н (А) зависит от статических свойств источника и метода кодирования сообщений, поступающих на вход канала. Энтропия Н (A | A *) характеризует потери информации в канале из-за воздействия помех и называется н е н а д е ж н о с т ь ю к а н а л а. Заметим, что потери информации при одном и том же уровне помех зависят также от методов модуляции и принятия решения. Таким образом, скорость передачи информации зависит от статических свойств источника (см. § 6-11), методов кодирования сообщений и свойств самого канала, т.е. она характеризует систему связи в целом.
Вследствие наличия избыточности в сообщениях и ненадежности канала связи скорость передачи информации 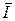 оказывается меньше (обычно много меньше) потока сообщений
оказывается меньше (обычно много меньше) потока сообщений  (см. § 6-2), в общем случае
(см. § 6-2), в общем случае 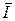 ≤
≤  . В связи с этим оказывается весьма важным определение максимально достижимых значений
. В связи с этим оказывается весьма важным определение максимально достижимых значений 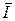 . Эти значения были определены Шенноном, который ввел понятие "пропускная способность канала".
. Эти значения были определены Шенноном, который ввел понятие "пропускная способность канала".
П р о п у с к н а я с п о с о б н о с т ь - это максимально возможная для данного канала скорость передачи информации
 (6-286)
(6-286)
При заданных характеристиках канала (основании кода q, длительность символов, ограничениях на передачу различных символов и вероятностях перехода) максимум в (6-286) находят по всем возможным источникам и способам кодирования сообщений. Поэтому пропускная способность не зависит от источника и фактической скорости передачи информации, а определяется только свойствами канала, т.е. ограничениями, накладываемыми на данный канал и шумами (ненадежностью канала). Следовательно, пропускная способность характеризует потенциальные возможности канала связи.
Важнейшим результатом теории информации является доказательство возможности передачи информации по данному каналу со скоростью, как угодно близкой к пропускной способности при сколь угодно высокой достоверности (малой вероятности ошибок в принятых сообщениях) и невозможности передачи информации с большей скоростью.
Для канала без шумов характерно однозначное соответствие передаваемых а и принимаемых а * символов, т.е а * ≡ а. Поэтому Н (A | A *) = 0 и скорость передачи информации по каналу равна
 (6-287)
(6-287)
Если кодирование производится однозначно, т.е. каждой последовательности сообщений соответствует вполне определенная последовательность кодовых символов, то скорость передачи 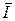 равна потоку информации источника
равна потоку информации источника  (6-278).
(6-278).
Пропускная способность канала без шумов определяется формулой
 (6-288)
(6-288)
Для стационарных каналов пропускная способность может быть выражена также через число всех возможных последовательностей N (T) символов длительностью Т при Т → ∞:

Рассмотрим некоторые случаи вычисления пропускной способности.
1. В канале используется код с основанием q. Длительность всех символов одинакова и равна τ. Ограничения на допустимую последовательность символов не накладываются. В этом случае N (T) = qn; T = nτ, где n - число символов в последовательности
 . (6-289)
. (6-289)
Таким образом, пропускная способность данного канала пропорциональна скорости передачи символов  (последняя зависит от полосы пропускания канала) и логарифму основания кода. Для того, чтобы в таком канале скорость передачи была равна пропускной способности, необходимо так закодировать сообщения источника, чтобы вероятности всех символов кода были одинаковы.
(последняя зависит от полосы пропускания канала) и логарифму основания кода. Для того, чтобы в таком канале скорость передачи была равна пропускной способности, необходимо так закодировать сообщения источника, чтобы вероятности всех символов кода были одинаковы.
2. В канале используется код с основанием q; длительности символов кода различны и равны τ 1, τ 2, …, τq. Ограничения на допустимую последовательность различных символов не накладываются. При этих условиях пропускная способность рассчитывается по формуле
 (6-290)
(6-290)
где τ 0 - произвольный отрезок времени, который удобно выбирать равным минимальной длительности символа; r 1 - наибольший действительный положительный корень уравнения
 (6-291)
(6-291)
Для достижения максимальной скорости передачи в рассматриваемой канале вероятности разных символов должны быть неравными: наиболее короткие символы должны иметь большие значения вероятностей в соответствии с формулой
 (6-292)
(6-292)
Формула (6-290) остается справедливой и в случае, когда на допустимую последовательность накладываются те или иные ограничения, однако при этом величина r 1 вычисляется иным образом [14].
Дата добавления: 2015-08-02; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Виды и классификация каналов связи | | | Код к примеру 1 |