Код к примеру 1

Сообщение	x 1	x 2	x 3	x 4
Код

Длительность символа кода τ = 1 мс. Определим пропускную способность канала, скорость передачи равновероятных сообщений и скорость передачи сообщений, имеющих различные вероятности: p (x ₁) = 0,5; p (x ₂) = 0,25; p (x ₃) = 0,125; p (x ₄) = 0,125.

Используя (6-289) при q = 2, получаем пропускную способность

C = 1/ τ = 1/10^-3 = 1000 дв.ед./с.

Скорость передачи равновероятных сообщений находим через энтропию источника и среднюю длительность кодовой комбинации < τ _к >. Так как сообщения равновероятны, то

H = log₂ 4 = 2 дв.ед./сообщ.;

< τ _к > = 2 τ = 2 ∙ 10^-3 c;

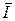= H / < τ _к > = 2/2 ∙ 10^-3 = 1000 дв.ед./с.

В соответствии с (6-245) находим энтропию и скорость передачи сообщений, имеющих различные вероятности:

дв.ед./сообщ.;

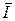= 1,75/2 ∙ 10^-3 = 875 дв.ед./с.

Следовательно, в рассматриваемом канале в случае равновероятных сообщений скорость передачи (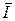 = С) будет максимально возможной. При этом утверждают, что источник согласован с каналом. При неравновероятных сообщениях скорость передачи меньше пропускной способности, т.е. данный источник не в полной мере реализует возможности канала.

Из теоремы Шеннона, которая приводится далее, следует, что для передачи сообщений второго источника достаточно иметь канал с меньшей пропускной способностью (С = 875 дв.ед./с). При этом необходимо будет применить эффективное кодирование.

2. Для передачи сообщений используются четыре различных символа с длительностями τ ₁ = 1 мс, τ ₂ = 2 мс, τ ₃ = τ ₄ = 3 мс. Ограничения на допустимую последовательность передачи символов не накладываются.

Определим пропускную способность канала и оптимальные статические характеристики кодированного сигнала.

Принимаем τ ₀ = τ ₁ = 1 мс. В соответствии с (6-291) запишем:

1 - r ^-1 - r ^-2 - 2 r ^-3 = 0.

Наибольший положительный корень этого уравнения r ₁ = 2.

В соответствии с (6-290)

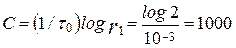дв.ед./с.

Для определения вероятностей передачи отдельных символов, при которых 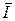= С, используем (6-292):

p (a ₁) = = 2^-1 = 0,5;

p (a ₂) = 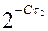= 2^-2 = 0,25;

p (a ₃) = p (a ₄) = 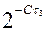= 2^-3 = 0,125

Результаты решения подтверждают положение, что для получения максимальной скорости передачи информации наиболее вероятным сообщениям должны соответствовать более короткие символы кода.

Теорема Шеннона для дискретного канала без шума. Если источник имеет энтропию Н (дв.ед/сообщение), а канал обладает пропускной способностью С (дв.ед/с), то сообщения источника можно закодировать таким образом, чтобы передавать их по каналу со средней скоростью С/Н - ε сообщений в секунду, где ε - сколь угодно малая величина.

Эта теорема дает ответ на вопрос о том, в какой мере скорость передачи информации может быть приближена к пропускной способности канала. Часто ее называют основной теоремой Шеннона о кодировании при отсутствии шума.

Другие формулировки этой теоремы:

1. Если = С - ε, то всегда можно закодировать достаточно длинное сообщение так, чтобы оно передавалось со скоростью 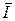= С - ε.

2. При кодировании множества сообщений с энтропией Н (Х) среднее количество символов кода < n >, приходящееся на одно сообщение, может быть сколь угодно близко (но не меньше) величины Н (Х) / log q, где q - основание кода, т.е.

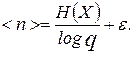(6-293)

При двоичном кодировании < n > = Н (Х) + ε.

Эффективное кодирование (сокращение избыточности). Кодирование сообщений, при котором достигается наилучшее использование пропускной способности канала (т.е. наибольшая скорость передачи информации), называется эффективным. Эффективность кодирования тем выше, чем меньше отличается средняя длительность кодовой комбинации < n > от величины Н (Х) / log q, где q - основание кода. Задача эффективного кодирования состоит в том, чтобы преобразовать последовательность элементов сообщения с избыточностью R_x в последовательность кодовых символов, не имеющую избыточности, либо имеющую значительно меньшую избыточность R_a < R_x; здесь

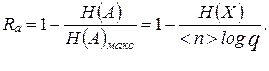(6-294)

При эффективном кодировании устраняется избыточность, обусловленная как неодинаковыми вероятностями элементов сообщений, так и статистическими связями между ними.

Если отдельные элементы сообщения (буквы) следуют независимо друг от друга, то избыточность может быть уменьшена (или устранена полностью) при кодировании путем представления наиболее вероятных элементов сообщения короткими кодовыми комбинациями, а менее вероятных - более длинными. Получаемый при этом код является неравномерным: кодовые комбинации для различных букв имеют разные длительности. Для декодирования на приемной стороне поступающую последовательность необходимо однозначно разделить на кодовые комбинации. Для этого необходимо, чтобы ни одна более короткая комбинация не являлась началом более длинной комбинации (свойство неприводимости). Например, если один из элементов сообщения закодирован двоичным кодом в виде последовательности 01101, то ни один из ее префиксов, т.е. 0110, 011, 01 и 0 не должен применяться для кодирования других элементов сообщения.

Среди различных способов построения неприводимых неравномерных кодов наибольшую известность получили методы Шеннона - Фано и Хаффмена [13, 14].

Построение двоичного кода Шеннона - Фано иллюстрирует табл. 6-15. Все буквы (сообщения) записываются в порядке убывания вероятностей их появления. Записанная последовательность разбивается (сверху вниз) на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности равными. Верхней группе присваивается цифра 0 в качестве первого символа кода, а нижней 1. Затем каждая группа разбивается на две подгруппы с соблюдением того же условия равенства суммы вероятностей. Верхним подгруппам в обеих группах опять присваивается цифра 0 (в качестве второго символа кода), а нижней 1. Деление на подгруппы продолжается до тех пор, пока в каждой подгруппе не окажется лишь по одной букве.

Таблица 6-15

Дата добавления: 2015-08-02