Примеры.

1. Определим пропускную способность двоичного симметричного канала связи, по которому передается 1000 симв/с при вероятности ошибки р_е = 0,1.

Непосредственно по (6-296) имеем:

С = 1000 (1 + 0,1 log 0,1 + 0,9 log 0,9) = 530 дв.ед./с.

Заметим, что при отсутствии шума пропускная способность канала равна 1000 дв.ед./с. Действие шума приводит к искажению в среднем 10 % символов (р_е = 0,1), однако пропускная способность снижается при этом почти на 47 %. Столь заметное различие в снижении пропускной способности по сравнению с долей неправильно принятых символов объясняется тем, что на приемной стороне неизвестно, какие именно символы приняты ошибочно. Остаточная неопределенность при этом равна 0,47 дв.ед./симв.

2. По каналу связи, состоящему из передатчика, ретранслятора и приемника (рис. 6-63), передаются символы а ₁ и а ₂ со скоростью . Значения априорных вероятностей и вероятностей перехода указаны на рисунке. Определим скорость передачи информации .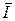

Рис. 6-63. Графы вероятностей переходов

в канале с ретранслятором.

Выразим скорость передачи через энтропию принимаемой последовательности

(6-301)

Найдем необходимые вероятности:

Вычислим энтропию Н (А *) и Н (А * | А):

Следовательно,

Заметим, что скорость передачи в данном случае равна пропускной способности, так как заданные априорные вероятности символов соответствуют максимуму выражения (6-301).

Теорема Шеннона для дискретного канала с шумом. Если поток информации , вырабатываемый источником, составляет = С - ε, где ε как угодно мало, а С - пропускная способность канала, то существует способ кодирования, при котором все сообщения, вырабатываемые источником, смогут быть переданы по каналу, а вероятность ошибочного опознания любого переданного сообщения может быть сколь угодно малой. Если > С, то не существует способа кодирования, обеспечивающего передачу всех сообщений с малой вероятностью ошибок.

Доказательство этой теоремы основано на фундаментальном свойстве эргодических последовательностей (см. § 6-10).

Наиболее важным является утверждение теоремы Шеннона о том, что в канале с шумами при сколь угодно малой вероятности ошибки скорость передачи может быть как угодно близкой к пропускной способности. До Шеннона существовало мнение, что при увеличении достоверности приема скорость передачи должна неограниченно уменьшаться, т.е. избыточность кодов должна неограниченно возрастать. Однако из теоремы Шеннона следует, что для достижения сколь угодно малой ошибки приема сообщений достаточно иметь избыточность , где ε - сколь угодно малая величина. Так, для примера в двоичном канале при передаче 1000 символ/с и вероятности искажения символа р_е = 10^-1 возможно передавать сообщения со скоростью ≈ 530 дв.ед./с при сколь угодно малой вероятности ошибки. При этом R _а ≈ 0,47.

К сожалению, теорема Шеннона не содержит указаний по конструированию кодов, реализующих эти возможности. Из ее доказательства лишь следует, что необходимо осуществлять кодирование достаточно длинных последовательностей сообщения.

В настоящее время однако уже найдены способы кодирования и декодирования сообщений, позволяющие достаточно близко подойти к пределам, указываемым этой теоремой (см. § 6-6).

Дата добавления: 2015-08-02