Розв’язання. 1) Знайдемо похідну від першого доданку за формулою:

1) Знайдемо похідну від першого доданку за формулою:

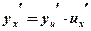, де .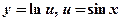

Тоді

.

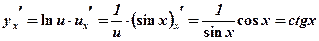Похідну від другого доданку знайдемо аналогічно:

.

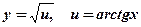
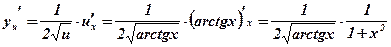Загалом

.

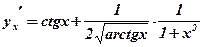2)

.

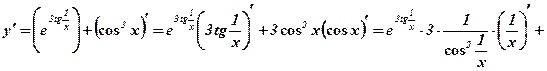
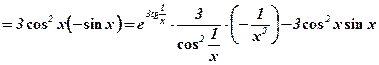3)

.

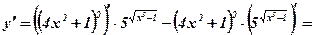
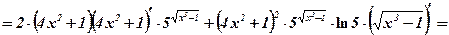
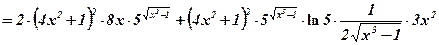4)

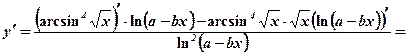
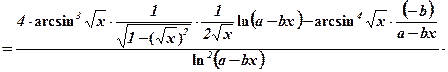
5) =

.

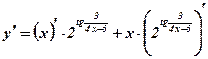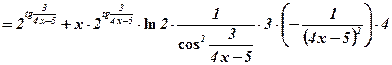Задача 4. Обчислити значення похідної функції 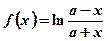у точці х=2а.

Розв’язання:

.

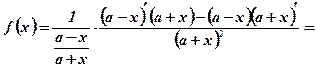
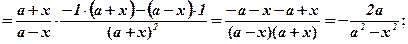
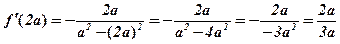Задача 5. Знайти похідну параметрично заданої функції:

, .

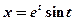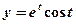Розв’язання. Знайдемо

;

;

.

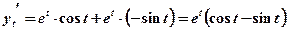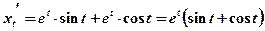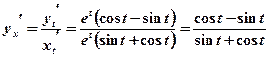Задача 6. Знайти похідну неявно заданої функції:

1) ;

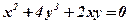2) .

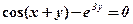1) Диференціюємо по х ліву і праву частину рівняння, враховуючи, що y – це функція від х:

.

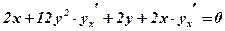Розв’язуємо рівняння відносно .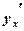

;

.

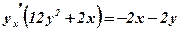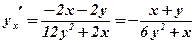2) Диференціюємо по х:

;

;

;

;

.

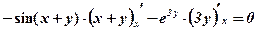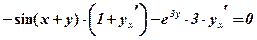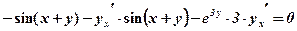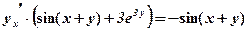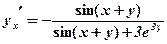Задача 7. Скласти рівняння дотичних до кривих:

1) 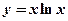у точці з абсцисою ;

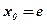2) 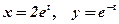у точці де, ;

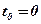3) 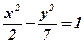у точці .

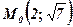Розв’язання:

1) Знайдемо кутовий коефіцієнт дотичної до кривої:

, ,

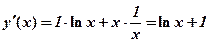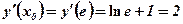а також .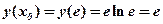

Підставимо в рівняння дотичної:

;

;

.

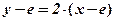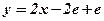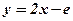2) .

;

.

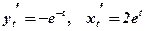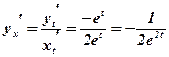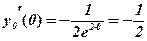Знайдемо координати точки М₀, через яку проведена дотична: , .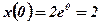

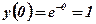Рівняння дотичної

;

.

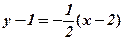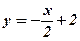3) Знайдемо похідну неявної функції:

;

;

.

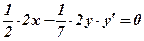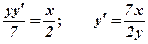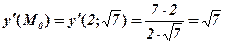Рівняння дотичної:

;

;

.

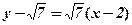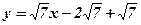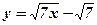Задача 8. Знайти похідну другого порядку функції:

1) ;

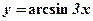2) ;

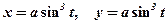3) .

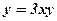Розв’язання:

1) Знайдемо

;

.

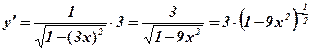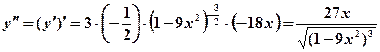2) ;

; ;

.

;

;

.

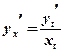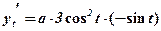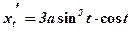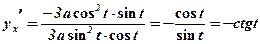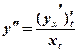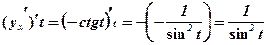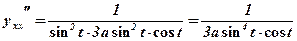3) ;

;

;

;

.

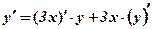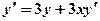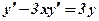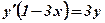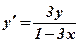Диференціюємо по х ще раз, а потім підставимо замість 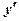її вираз через х.

.

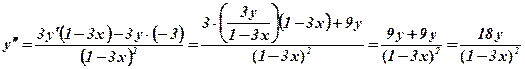Завдання для самостійної роботи.

1. Знайти похідні функцій:

1) ;

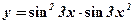2) ;

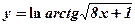3) ;

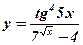4) .

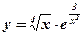2. Обчислити значення похідної 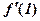функції .

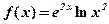3. Знайти похідні параметричної і неявної функцій:

1) ;

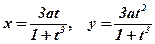2) .

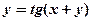4. Скласти рівняння дотичних до кривих:

1) 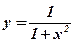у точці з абсцисою х₀=0;

2) ;

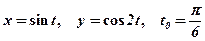3) 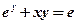у точці М(0;1).

5. Знайти другі похідні функцій:

1) ;

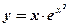2) ;

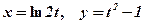3) .

---

Дата добавления: 2015-07-20