
|
Читайте также: |
За означенням суми і різниці векторів маємо:  ,
, 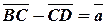 . Додавши ці рівності, дістанемо
. Додавши ці рівності, дістанемо  . Далі знайдемо
. Далі знайдемо  ;
;  ,
,  .
.
Задача 3. Дано: 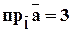 ;
;  . Обчислити: 1)
. Обчислити: 1)  ; 2)
; 2)  .
.
Розв’язання. Використавши властивості проекцій, дістанемо:
1)  .
.
2) 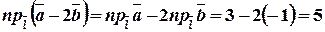 .
.
Задача 4. Знайти проекції вектора 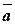 на вісь l, яка утворює з вектором кут: 1) 450, 2) 1200, 3) 1500, якщо довжина вектора дорівнює 4.
на вісь l, яка утворює з вектором кут: 1) 450, 2) 1200, 3) 1500, якщо довжина вектора дорівнює 4.
Розв’язання.
1) 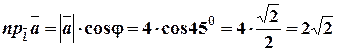 ;
;
2)  ;
;
3) 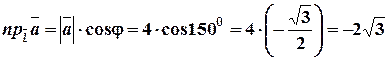 .
.
Задача 5. Знайти периметр трикутника, вершинами якого є точки  ,
,  ,
,  .
.
Розв’язання. Знайдемо координати векторів, що створюють трикутник, та їх довжини:
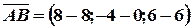 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
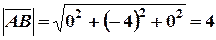 ;
;
 ;
;
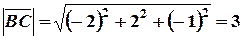 .
.
Тоді периметр трикутника  .
.
Задача 6. Обчислити довжину вектора  , якщо
, якщо  ,
,  .
.
Розв’язання. Знайдемо координати векторів:
 ,
,  ;
;
 ,
,  ;
;
 ,
, 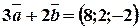 .
.
Тоді довжина шуканого вектора дорівнює:
 .
.
Задача 7. Відрізок АВ, де  ,.
,. 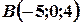 , поділений точкою М у відношенні
, поділений точкою М у відношенні 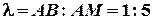 . Знайти координати точки М.
. Знайти координати точки М.
Розв’язання.
 ;
;  ;
;
 .
.
Отже,  .
.
Задача 8. Відрізок з кінцями  і
і 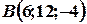 , ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де
, ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де  .
.
Розв’язання. Знайдемо координати точки М за формулами:
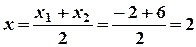 ;
;  ;
;  ;
;
 .
.
Тоді координати вектора  ,
,  .
.
Довжина вектора  .
.
Задача 9. Точки  ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D.
 |
Позначимо координати точки  , тоді
, тоді  ,
,  . Оскільки
. Оскільки  , їх координати рівні:
, їх координати рівні:
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Четверта вершина паралелограма – точка  .
.
Задача 10. Знайти напрямні косинуси вектора 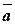 , а також кути, що утворює вектор з осями координат, якщо
, а також кути, що утворює вектор з осями координат, якщо  .
.
Розв’язання. Знайдемо координати вектора 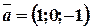 та його довжину
та його довжину 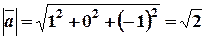 .
.
Напрямні косинуси дорівнюють:
 ;
;  ;
; 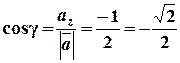 .
.
Тоді  ;
;  ;
; 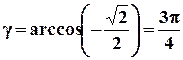 .
.
Завдання для самостійної роботи.
Задача 1. У трикутнику АВС проведено медіану АМ. Доведіть, що  .
.
Задача 2. Дано вектори  ,
,  ,
, 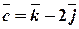 . Знайти довжини векторів 1)
. Знайти довжини векторів 1)  , 2)
, 2)  .
.
Задача 3. Точки 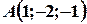 ,
,  ,
,  є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму.
є вершинами паралелограма, причому А і С – протилежні вершини. Знайдіть четверту вершину D, а також периметр паралелограму.
Задача 4. Дано:  ,
,  , кути між віссю l дорівнюють 600 і 1200. Обчислити
, кути між віссю l дорівнюють 600 і 1200. Обчислити  .
.
Задача 5. Відрізок АВ задано координатами своїх кінців  і
і 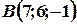 . Знайти довжину вектора
. Знайти довжину вектора 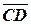 , де С – середина відрізка АВ, D – точка, яка ділить АВ у відношенні
, де С – середина відрізка АВ, D – точка, яка ділить АВ у відношенні 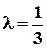 .
.
4. Скалярний, векторний, мішаний добутки векторів. Застосування в задачах геометрії. Умови перпендикулярності та компланарності векторів.
1. Скалярним добутком векторів називається число, що дорівнює добутку довжин векторів на косинус кута між ними:

Якщо вектори задані своїми координатами:  ,
,  , то скалярний добуток обчислюють за формулою:
, то скалярний добуток обчислюють за формулою:
 .
.
Кут між векторами обчислюють за формулою:
 .
.
Умова перпендикулярності векторів 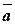 і
і  має вигляд:
має вигляд:
 .
.
Скалярний квадрат вектора дорівнює:
 .
.
Проекція вектора 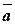 на напрям вектора
на напрям вектора  :
:
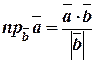 .
.
2. Векторним добутком двох векторів 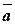 і
і  називається третій вектор
називається третій вектор  , який задовольняє умові:
, який задовольняє умові:
1)  ;
;
2)  ,
,  ;
;
3)
 |
 утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора
утворюють праву трійку векторів, тобто третій вектор має такий напрям, що при спостереженні з його кінця найближчий поворот від вектора 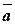 до
до  виконується проти годинникової стрілки.
виконується проти годинникової стрілки.
Векторний добуток позначається символом 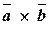 . За визначенням випливає, що
. За визначенням випливає, що  .
.
Модуль векторного добутку дорівнює площі паралелограма, побудованого на 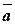 і
і  :
:
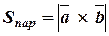 .
.
Площа трикутника обчислюється за формулою:
 .
.
Векторній добуток векторів, які задані своїми координатами, обчислюються за формулою:
 .
.
Умова колінеарності двох векторів 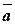 і
і  має вигляд:
має вигляд:
 (або
(або 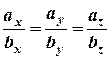 ).
).
Векторні добутки ортів дорівнюють:
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
3. Мішаним добутком трьох векторів називається добуток  .
.
Частіше мішаний добуток позначається 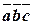 .
.
Якщо вектори задані своїми координатами, то мішаний добуток знаходять за формулою:
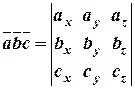 .
.
Об’єм паралелепіпеду, який побудований на векторах  ,
,  ,
,  як на сторонах, дорівнює модулю мішаного добутку цих векторів:
як на сторонах, дорівнює модулю мішаного добутку цих векторів:
 .
.
Для об’єму піраміди маємо наступну формулу:
 .
.
Умова компланарності трьох векторів має вигляд:  .
.
Дата добавления: 2015-07-20; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Властивості проекції. | | | Зразки розв’язування задач. |