Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Матричний метод роз’язання лінійних систем.

Основні властивості визначників. | Зразки розв’язування задач. | Обчислити визначник , розклавши його за елементами першого рядка. | Знайти матрицю, обернену до матриці і перевірити, чи справджуються рівності . | Додавання векторів. | Проекція вектора на вісь. | Властивості проекції. | Розв’язання. | Зразки розв’язування задач. | Розв’язання. |


Читайте также:
  1. CПОСОБИ ПОБУДОВИ ШТРИХОВИХ КОДІВ ТА МЕТОДИ КЛАСИФІКАЦІЇ
  2. D. Лабораторні методи
  3. I. . Психология как наука. Объект, предмет и основные методы и психологии. Основные задачи психологической науки на современном этапе.
  4. I. Культурология как наука. Предмет. Место. Структура. Методы
  5. I. МЕТОД
  6. I. Методы исследования ПП
  7. I.Методы формирования соц-го опыта.

Нехай дано систему:

Розглянемо три матриці:

 

Перша матриця називається матрицею симтеми, друга матрицею-стовпцем змінних, третя – матрицею-стовпцем вільних членів. Тоді систему можна записати у матричному вигляді: 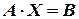. Якщо матриця системи рівнянь невироджена , то розв’язок системи знаходимо у вигляді , або

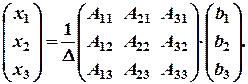
Дата добавления: 2015-07-20; просмотров: 81 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Для заданої матриці знайти обернену: .| Зразки розв’язування задач.
mybiblioteka.su - 2015-2024 год. (0.008 сек.)