Розв’язання. 1) Перевіримо виконання умови

1) Перевіримо виконання умови . Для даних прямих: ; ; ; . Тоді 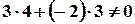. Це означає, що прямі неперпендикулярні.

2) Якщо прямі задані рівняннями з кутовими коефіцієнтами, то умова перпендикулярності має вигляд: 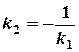. Кутові коефіцієнти даних прямих дорівнюють: ; 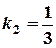. Умова перпендикулярності не виконується, отже, прямі неперпендикулярні.

3) Рівняння першої прямої запишемо у вигляді: 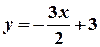. Тоді . Друга пряма має кутовий коефіцієнт: 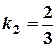. Умова перпендикулярності виконується: 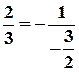; . Прямі перпендикулярні.

Задача 7. Складіть рівняння прямої, яка проходить через точку перпендикулярно до прямої .

Розв’язання. Знайдемо кутовий коефіцієнт даної прямої: 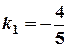. Тоді кутовий коефіцієнт шуканої прямої . Отже її рівняння має вигляд , або .

Задача 8. Знайдіть відстань від точки до прямої .

Розв’язання. Використовуючи формулу для обчислювання відстані від точки до прямої, дістанемо:

.

Задача 9. Знайдіть відстань між двома паралельними прямими і .

Розв’язання. Знайдемо будь-яку точку на першій прямій. Якщо візьмем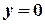о , то . Тоді 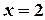. Таким чином, точка належить першій прямій. Отже, відстань від цієї точки до прямої обчислюється за формулою 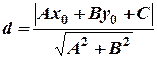. Одержуємо .

Завдання для самостійної роботи.

1.Складіть рівняння прямих, які проходять через точку 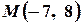під кутом до прямої .

2.Знайдіть рівняння двох перпендикулярів до прямої у точках перетину її з осями координат.

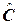3.Трикутник задано вершинами , і . Знайдіть: кути і ;рівняння висоти, яка проведена з вершини 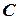; довжину перпендикуляра до сторони , який проходить через вершину .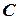

4. Дві протилежні вершини квадрата лежать у точках 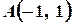і .Складіть рівняння сторін і діагоналей цього квадрата.

Дата добавления: 2015-07-20