Розв’язання.

1) Кутові коефіцієнти даних прямих дорівнюють 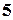і . Тангенс куту між прямими беремо за модулем: . Отже .

2) Косинус кута між прямими беремо за модулем: . Отже .

Задача 2. Дано трикутник з вершинами , і . Знайдіть внутрішні кути цього трикутника.

Розв’язання. Знаходимо кутові коефіцієнти сторін цього трикутника:

; ;

.

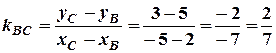Знайдемо кути трикутника:

; ;

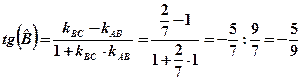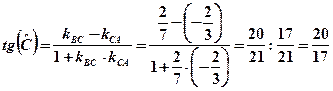. Отже ; ; .

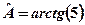Задача 3. Які з прямих паралельні?

; ; ; .

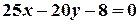Розв’язання. Паралельні прямі мають однакові кутові коефіцієнти. Знайдемо кутові коефіцієнти прямих: ; ; ; . Таким чином, , а це означає, що перша та друга прямі – паралельні.

Задача 4. Складіть рівняння прямої, яка проходить через точку 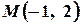паралельно прямій .

Розв’язання. Знайдемо кутовий коефіцієнт даної прямої: ; ; .

Оскільки дана і шукана прямі паралельні, то їх кутові коефіцієнти рівні, тобто . Шукана пряма проходить через точку 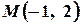і має кутовий коефіцієнт . Тоді її рівняння запишемо у вигляді: , або .

Задача 5. При якому значенні параметра 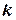прямі і перпендикулярні?

Розв’язання. Кутові коефіцієнти перпендикулярних прямих зв’язані між собою співвідношенням: . Для даних прямих: . Звідки, .

Задача 6. Перевірте, чи перпендикулярні прямі:

1) і ;

2) і ;

3) і .

Дата добавления: 2015-07-20