
Читайте также:
|
Задача 1. Перевірити, чи належать точки 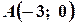 ,
, 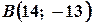 ,
, 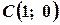 ,
, 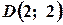 прямій
прямій 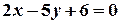 .
.
Розв’язання. Якщо координати точки задовольняють рівнянню, тобто перетворюють його в тотожність, то ця точка належить заданій прямій; якщо координати точки не задовольняють рівнянню, то точка не належить прямій.
Підставивши замість змінних 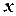 і
і 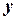 в рівняння
в рівняння 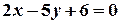 координати точки
координати точки 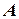 , дістанемо тотожність
, дістанемо тотожність 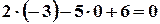 , отже точка
, отже точка 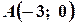 належить заданій прямій. Аналогічно переконуємося у тому, що точка
належить заданій прямій. Аналогічно переконуємося у тому, що точка 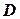 належить прямій, а точки
належить прямій, а точки 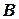 і
і 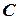 не належать.
не належать.
Задача 2. Побудуйте прямі:
a) 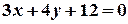 ;
;
б) 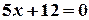 ;
;
в) 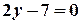 .
.
Розв’язання.
 |
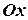 і
і 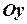 . Припустивши, що
. Припустивши, що 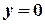 , дістанемо
, дістанемо 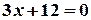 ,
, 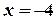 ,
, 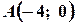 . При
. При 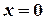 дістанемо
дістанемо 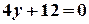 ,
, 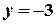 ,
, 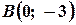 . Через точки
. Через точки 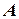 і
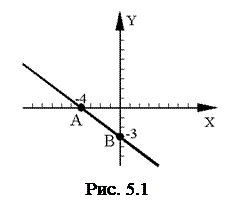
і 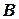 проводимо шукану пряму (рис. 5.1).
проводимо шукану пряму (рис. 5.1).
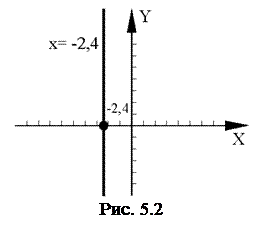
б) Знайдемо змінну 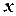 з рівняння
з рівняння 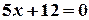 :
: 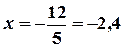 . На осі
. На осі 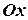 візьмемо точку
візьмемо точку 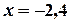 і проведемо пряму паралельно осі
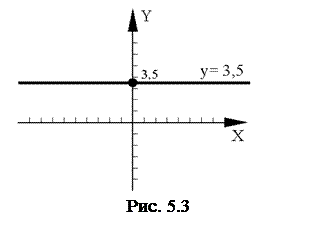
і проведемо пряму паралельно осі 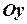 (рис. 5.2).
(рис. 5.2).
 |
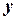 з рівняння
з рівняння 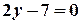 :
: 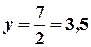 .
.
 |
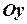 візьмемо точку
візьмемо точку 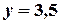 і проведемо пряму паралельно осі
і проведемо пряму паралельно осі 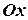 (рис. 5.3)
(рис. 5.3)
Задача 3. Складіть рівняння прямої, що проходить через точку 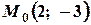 і паралельна вектору
і паралельна вектору 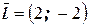 .
.
Розв’язання. Використовуючи канонічне рівняння прямої, маємо 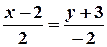 .
.
Доводимо рівняння до загального вигляду:

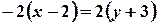 ;
; 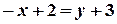 ;
; 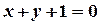 .
.
Задача 4. Загальне рівняння прямої 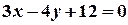 перетворити в рівняння у відрізках на осях та побудувати пряму.
перетворити в рівняння у відрізках на осях та побудувати пряму.
Розв’язання. Перетворимо рівняння: 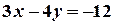 . Праву та ліву частини рівняння розділимо на
. Праву та ліву частини рівняння розділимо на 
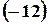 :
: 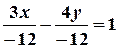 .
.
Тоді 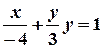 - рівняння у відрізках на осях.
- рівняння у відрізках на осях.
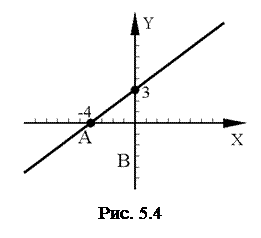 |

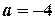 і
і 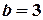 . Отже дістанемо точки
. Отже дістанемо точки 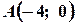 і
і 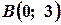 . Пряма, яка проведена через точки
. Пряма, яка проведена через точки 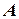 і
і 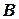 - шукана (рис. 5.4).
- шукана (рис. 5.4).
Задача 5. Обчислить кутовий коефіцієнт прямої 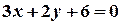 .
.
Розв’язання. Розв’язавши рівняння 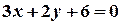 відносно
відносно 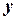 , дістанемо
, дістанемо 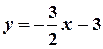 , звідки
, звідки 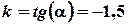 .
.
 Задача 6. Складіть рівняння прямої, яка проходить через точку
Задача 6. Складіть рівняння прямої, яка проходить через точку 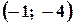 і утворює з віссю
і утворює з віссю 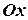 кут 1350.
кут 1350.
Розв’язання. Щоб скласти шукане рівняння прямої, треба знайти 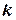 і
і 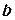 . Знайдемо кутовий коефіцієнт
. Знайдемо кутовий коефіцієнт 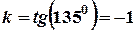 . Для визначення
. Для визначення 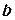 підставимо в рівняння з кутовим коефіцієнтом
підставимо в рівняння з кутовим коефіцієнтом 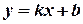 координати даної точки і значення
координати даної точки і значення 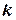 . Дістанемо:
. Дістанемо: 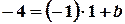 , звідки
, звідки 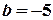 . Шукане рівняння має вигляд
. Шукане рівняння має вигляд 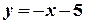 .
.
Задача 7. Складіть рівняння прямої, яка проходить через точки 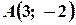 і
і 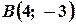 .
.
Розв’язання. За умовою задачі: 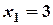 ,
, 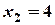 ,
, 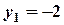 ,
, 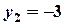 . Підставивши ці значення в рівняння прямої, яка проходить через дві точки, дістанемо:
. Підставивши ці значення в рівняння прямої, яка проходить через дві точки, дістанемо: 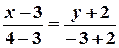 ;
; 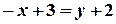 і
і 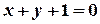 .
.
Задача 8. Трикутник задано вершинами: 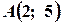 ,
, 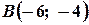 .і
.і 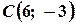 . Складіть рівняння медіани
. Складіть рівняння медіани 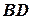 .
.
Розв’язання. Знайдемо координати точки 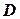 - середини сторони
- середини сторони 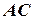 :
:
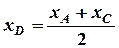 ;
; 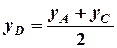 ;
;
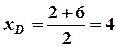 ;
; 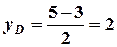 .
.
Отже, координати точки дорівнюють 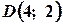 . Тоді рівняння сторони
. Тоді рівняння сторони 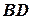 , де
, де 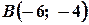 , має вигляд:
, має вигляд: 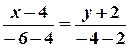 ;
;
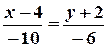 ;
;
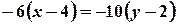 ;
;
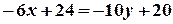 ;
;
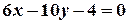 ;
;
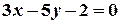 .
.
Задача 9. Знайдіть вершини трикутника, якщо його сторони задано рівняннями. 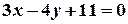 ;
; 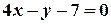 ;
; 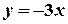 .
.
Розв’язання. Щоб знайти координати вершин трикутника, треба розв’язати три системи рівнянь:
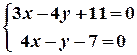
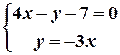
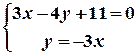 .
.
Перша система має розв’язок:
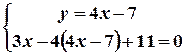
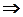
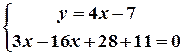
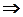
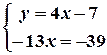
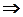
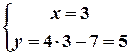
Друга система має розв’язок:
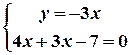
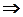
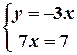
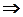
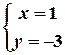 .
.
Третя система має розв’язок:
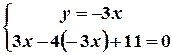
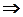
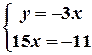
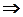
 .
.
Отже, вершинами трикутника є точки 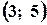 ;
; 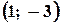 ;
; 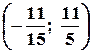 .
.
Завдання для самостійної роботи.
1. При якому значенні коефіцієнта 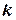 пряма
пряма 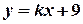 проходить через точку перетину прямих
проходить через точку перетину прямих 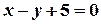 і
і 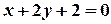 .
.
2. Пряма проходить через точку 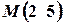 і утворює з віссю
і утворює з віссю 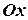 кут, що дорівнює
кут, що дорівнює 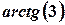 . Знайдіть на цій прямій точку з абсцисою
. Знайдіть на цій прямій точку з абсцисою 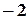 .
.
3. Дано рівняння сторін трикутника: 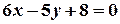 ;
; 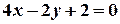 і
і 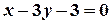 . Знайдіть рівняння його медіан.
. Знайдіть рівняння його медіан.
4. На прямій 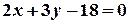 знайдіть точку, яка лежить від осі в три рази далі, ніж від осі
знайдіть точку, яка лежить від осі в три рази далі, ніж від осі 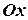 .
.
5. Складіть рівняння прямої, яка перпендикулярна до даного вектора і проходить через точку перетину даних прямих:
a) 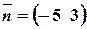 ,
, 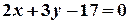 ;
; 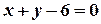 .
.
b) 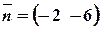 ;
; 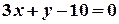 ;
; 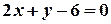 .
.
6. Кут між двома прямими. Пучок прямих, які проходять через дану точку. Нормальне рівняння прямої. Відстань від точки до прямої.
Кут 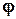 між двома прямими, які задані загальними рівняннями
між двома прямими, які задані загальними рівняннями 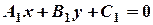 і
і 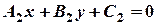 , обчислюється за формулою:
, обчислюється за формулою:
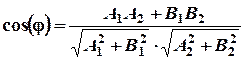 .
.
Якщо прямі задані рівняннями 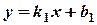 і
і 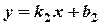 , то кут між прямими обчислюється за формулою
, то кут між прямими обчислюється за формулою 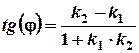 .
.
Умова паралельності двох прямих: 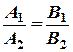 ;
; 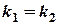 .
.
Умова перпендикулярності двох прямих: 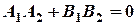 ;
; 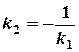 .
.
Рівняння пучка прямих, які проходять через дану точку 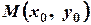 , має вигляд:
, має вигляд: 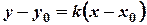 .
.
Нормальне рівняння прямої 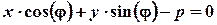 одержуємо з загального рівняння
одержуємо з загального рівняння 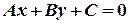 , якщо останнє поділити на
, якщо останнє поділити на 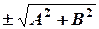 і вибрати знак протилежний знаку
і вибрати знак протилежний знаку 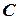 .
.
Відстань від точки 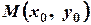 до прямої
до прямої 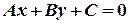 обчислюється за формулою:
обчислюється за формулою: 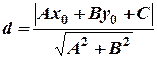 .
.
Зразки розв’язування задач.
Задача 1. Знайти гострий кут між прямими:
1) 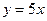 і
і 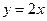 .
.
2) 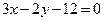 і
і 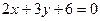 .
.
Дата добавления: 2015-07-20; просмотров: 161 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розв’язання. | | | Розв’язання. |