|
Читайте также: |
Похідною функції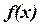 
в точці 
називається границя відношення приросту функції 
функції в цій точці до приросту 
аргументу, коли приріст аргументу прямує до нуля:
Наводимо таблицю похідних основних елементарних функцій.
1. 
2. 
3. 
4. 
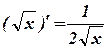
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
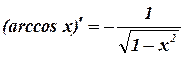
13. 
14. 
15. 
16. 
При знаходженні похідної функції користуються також основними правилами диференціювання.
1. 
, де с – стала.
2. 
, де 
- функція.
3. 
.
4. 
.
Якщо у є функція від : 
, де , у свою чергу є функція від аргументу х: 
, тобто залежить від х через проміжний аргумент , у називається складеною функцією від х (функцією від функції): 
.
Похідна складеної функції дорівнює добутку її похідної за проміжним аргументом на похідну цього аргументу за незалежною змінною:
.
Якщо функція у від х задана параметричними рівняннями 
, 
(
- параметр), похідна 
обчисляється за формулою 
.
Геометричний зміст похідної 
у точці 
у тому, що вона дорівнює кутовому коефіцієнту дотичної до кривої 
у точці з абсцисою . Рівняння дотичної до кривої в точці з абсцисою має вигляд:
.
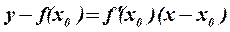Другою похідною функції називається похідна від першої похідної цієї функції:
.
Друга похідна параметрично заданої функції обчисляється за формулою:
.
Дата добавления: 2015-07-20; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нескінченна числова послідовність. Границя числової послідовності і її властивості. Нескінченно малі і нескінченно великі послідовності. | | | Розв’язання. |