Читайте также:
|
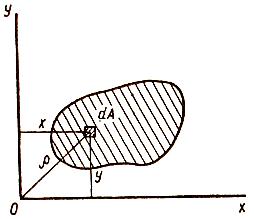
Представим, что сечение разделено на множество элементарных площадок dA (см. рис. – изображена одна из них), координаты которых x и y. Тогда интегралы
и 
Называются моментами инерции сечения относительно осей x и y, а интеграл 
принято называть центробежным моментом инерции сечения относительно осей x и y.
Величина площади dA положительна, поэтому независимо от знака координаты x или y осевые моменты инерции всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным в зависимости от расположения сечения относительно осей x или y.
Зависимость между осевыми и полярными моментами инерции
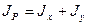
Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Моменты инерции относительно осей, проходящих через центр тяжести сечения, называются центральными.
Дата добавления: 2015-07-25; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрические характеристики брусьев круглого, поперечного сечения при кручении. Потенциальная энергия деформации при кручении. | | | Прямоугольное сечение. |