Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси x
Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим
Окончательно
Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:
39. Круглое сечение
Для круга главные центральные моменты инерции относительно осей x и y равны между собой.
Поэтому из равенства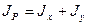 
, получаем
или 
,
где 
.
Подставим значение Jp и получим для круглого сечения 
Дата добавления: 2015-07-25; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Моменты инерции сечения. Вычисление моментов инерции брусьев прямоугольного и круглого сечения. | | | Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры. Дифференциальные зависимости при изгибе. |