
|
Читайте также: |
Обчислюємо параметр а 0.
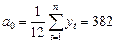 .
.
подальший розрахунок значень функції гармонічного ряду наведено в табл. 2.4.
На рисунку 2.1 показані емпіричний і теоретичний (для т = 1, 2, 3 гармоніки) графіки змінювання кількості перевезених пасажирів за період 12 місяців.
Теоретична модель змінювання обсягів перевезень пасажирів на маршруті описується наступним рівнянням
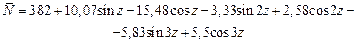
де  .
.
Таблиця 2.5 – Розрахунок значень функції гармонічного ряду для т = 3 гармонік
| Номер гармоніки | Складові елементи функції | Періоди часу t | ak | bk | s k | |||||||||||
| yt sin kt | 296,1 | 327,3 | -199 | -348,1 | -384 | -331,1 | -188 | а 1 = -10,07 | b 1 = -15,48 | 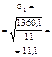
| ||||||
| yt cos kt | 311,7 | -189 | -336 | -403 | -344,7 | -201 | 191,5 | 325,6 | ||||||||
| a 1sin kt | -5,03 | -8,71 | -10,07 | -8,71 | -5,03 | 5,03 | 8,71 | 10,07 | 8,71 | 5,03 | ||||||
| b 1cos kt | -13,41 | -7,74 | 7,74 | 13,41 | 15,48 | 13,41 | 7,74 | -7,74 | -13,41 | -15,48 | ||||||
| 363,6 | 365,6 | 371,9 | 390,4 | 397,5 | 400,4 | 398,5 | 392,1 | 373,6 | 366,5 | ||||||
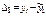
| -3,6 | -23,6 | 21,1 | -3 | -2,4 | 5,5 | -2,4 | 3,5 | -8,1 | 2,4 | 14,5 | |||||
| yt sin kt | 311,7 | 296,1 | -327,3 | -336 | 344,7 | 348,1 | -331,7 | -325,6 | а 2 = -3,33 | b 2 = 2,58 | 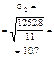
| |||||
| yt cos kt | -171 | -393 | -189 | -201 | -384 | -191,5 | ||||||||||
| a 2sin kt | -2,88 | -2,88 | 2,88 | 2,88 | -2,88 | -2,88 | 2,89 | 2,88 | ||||||||
| b 2cos kt | 1,29 | -1,29 | -2,58 | -1,29 | 1,29 | 2,58 | 1,29 | -1,29 | -2,58 | -1,29 | 1,29 | 2,58 | ||||

| 361,4 | 369,3 | 382,6 | 394,6 | 400,1 | 398,8 | 394,3 | 389,5 | 384,6 | 377,8 | 369,1 | |||||
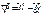
| -2 | -19,4 | 23,7 | -4,6 | -6,6 | 2,3 | -0,8 | 7,7 | -5,5 | -1,6 | -1,8 | 11,9 | ||||
| yt sin kt | -393 | -398 | -376 | а 3 = -5,83 | b 3 = 5,5 | 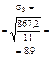
| ||||||||||
| yt cos kt | -342 | -403 | -383 | |||||||||||||
| a 3sin kt | -5,83 | 5,83 | 5,83 | 5,83 | -5,83 | 5,83 | ||||||||||
| b 3cos kt | -5,5 | 5,5 | -5,5 | 5,83 | -5,83 | 5,83 | ||||||||||

| 356,2 | 355,9 | 375,1 | 388,1 | 388,8 | 394,6 | 404,6 | 399,8 | 383,7 | 379,1 | 383,6 | 374,6 | ||||
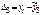
| 3,8 | -13,9 | -10,1 | -0,8 | 8,4 | -6,6 | 2,2 | 0,3 | 3,9 | -7,6 | 6,4 |
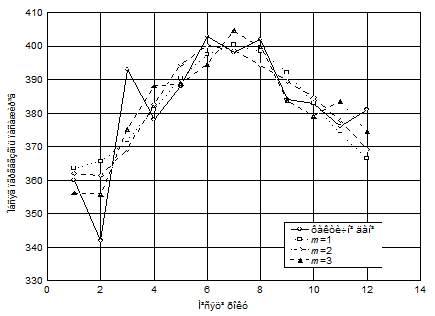
Рисунок 2.1 – Згладжування часового ряду рядами Фур’є
з різною кількістю гармонік
Контрольні запитання
1. Наведіть приклади статистично змінюваних техніко-економічних показників та транспортних процесів, що мають сезонну складову.
2. У яких випадках для згладжування динамічного ряду застосовують гармонічні ряди?
3. Дайте визначення гармоніки ряду.
4. Як залежить максимальна кількість гармонік ряду Фур’є від кількості рівнів динамічного ряду?
5. Як обчислюються гармонічні коефіцієнти ряду?
6. За якою ознакою визначається кількість гармонік, що включається у будовану математичну модель?
Дата добавления: 2015-07-20; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Зміст практичного заняття та вихідні дані до його виконання | | | Стисла теоретична довідка |