Розв’язок. Приклад побудови прогнозної моделі за методом ковзної середньої наведений в таблиці

Приклад побудови прогнозної моделі за методом ковзної середньої наведений в таблиці 1.2. Згладжування обсягів переробки вантажів виконано три- (m = 3) і п’ятичленними (m = 5) ковзними середніми. Значення для періоду t = 12 (для m = 3) та періодів t =11 та t = 12 (для m = 5) розраховувались за формулою (1.3), а для (t + τ) = (12 + 1)... (12 + 3) – за формулою (1.5). У другому стовпчику таблиці через дріб наведені екстрапольовані дані про значення показника за межею області спостережень (чисельник – тричленна ковзна середня, знаменник – п’ятичленна ковзна середня).

Таблиця 1.2 – Розрахунки прогнозу методом ковзної середньої

Місяці року t	Обсяги переробки вантажів уt , тис.т.	m = 3	m = 5
сума			сума
	10,3	–	–	–	–	–
	14,3	32,3	10,8	12,25	–	–
	7,7	37,8	12,6	24,01	62,5	12,5	23,0
	15,8	37,9	12,6	10,89	68,9	13,8	4,0
	14,4	44,6	15,6	1,44	69,9	14,0	0,16
	16,7	47,8	15,5	1,44	82,4	16,5	0,04
	15,3	52,2	17,4	0,92	83,7	16,7	1,96
	20,2	52,6	17,5	7,29	76,8	15,4	23,0
	17,1	44,8	14,9	4,84	76,5	15,1	4,0
	7,5	40,1	13,4	34,81	76,8	15,4	62,4
	15,5	39,5	13,2	5,29	–	11,1	19,4
	16,5	–	13,0	12,25	–	10,1	40,9
(τ = 1)	13,0 / 10,1	–	14,8	–	–	8,08	–
(τ = 2)	14,8 / 8,08	–	14,6	–	–	6,28	–
(τ = 3)	14,6 / 6,28	–	14,0	–	–	6,04	–
				115,43			178,97

За результатами розрахунків будуємо графіки вихідного динамічного ряду та згладжених при m = 3 та m = 5 (рисунок 1.1).

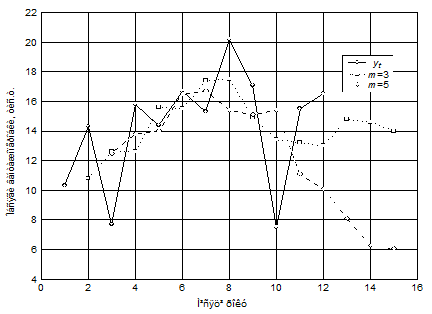
Рисунок 1.1 – Згладжування часового ряду тричленною та п’ятичленною ковзною середньою

Розраховуємо похибку прогнозу:

для тричленної ковзної середньої

; ;

для п’ятичленної ковзної середньої

; .

Побудову прогнозної моделі за методом експоненціального згладжування проводимо у наведеній нижче послідовності.

Лінійна функція прогнозу.

1. Визначаємо константу згладжування a:

тут т – кількість точок (рівнів) ряду динаміки.

2. Для першої точки (t = 1) приймаємо значення змінної згладжування відповідно першого і другого порядку:

.

3. Розраховуємо експоненціальні середні для другої точки (t = 2) за формулами:

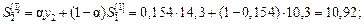
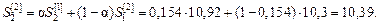
4. обчислюємо коефіцієнти а ₀(t) і а ₁(t) для другої точки (t = 2):

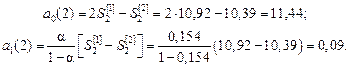
5. Визначаємо прогнозне значення для другої точки (t = 1):

.

6. Аналогічно обчислюємо , , 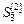коефіцієнти а ₀(3) і а ₁(3), прогнозне значення 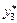і т. д. до кінцевого періоду t = 12. Результати розрахунків наведені в таблиці 1.3.

Таблиця 1.3 – Розрахунки прогнозу методом експоненціального згладжування (лінійна функція прогнозу)

Місяці року t	Обсяги переробки вантажів уt , тис.т.
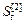
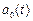
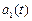
	10,3	10,30	10,30	–	–	–	–
	14,3	10,92	10,39	11,44	0,09	11,53	7,66
	7,7	10,42	10,40	10,44	0,00	10,45	7,54
	15,8	11,25	10,53	11,97	0,13	12,10	13,69
	14,4	11,73	10,72	12,75	0,19	12,94	2,13
	16,7	12,50	10,99	14,01	0,27	14,28	5,84
	15,3	12,93	11,29	14,57	0,30	14,87	0,18
	20,2	14,05	11,71	16,39	0,43	16,81	11,48
	17,1	14,52	12,15	16,89	0,43	17,33	0,05
	7,5	13,44	12,35	14,53	0,20	14,73	52,29
	15,5	13,76	12,56	14,95	0,22	15,17	0,11
	16,5	14,18	12,81	15,55	0,25	15,79	0,50
(τ = 1)	15,79	14,43	13,06	15,79	0,25	16,04	–
(τ = 2)	16,04	14,68	13,31	16,04	0,25	16,29	–
(τ = 3)	16,29	14,92	13,56	16,29	0,25	16,54	–
							101,49

7. Для періоду t = 13 (t = 1) приймаємо . Далі розраховуємо , , 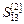коефіцієнти а ₀(13) і а ₁(13), прогнозне значення . Аналогічним чином діємо для рівнів t = 14 та t = 15.

8. Розраховуємо стандартну похибку часового ряду

;

9. Розраховуємо похибку прогнозу

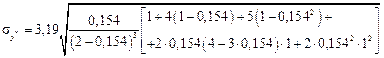= 1,19.

Квадратична функція прогнозу.

1. Для першої точки (t = 1) приймаємо значення змінної згладжування відповідно першого, другого і третього порядку:

.

2. Розраховуємо експоненціальні середні для другої точки (t = 2) за формулами:

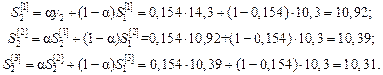
3. обчислюємо коефіцієнти а ₀(t) і а ₁(t) для другої точки (t = 2):

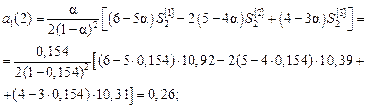
4. Визначаємо прогнозне значення для другої точки (t = 1):

.

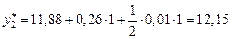5. Аналогічно обчислюємо , , 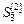коефіцієнти а ₀(3), а ₁(3) і а ₂(3), прогнозне значення 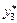і т. д. до кінцевого періоду t = 12. Результати розрахунків наведені в таблиці 1.4.

Таблиця 1.3 – Розрахунки прогнозу методом експоненціального згладжування (квадратична функція прогнозу)

Місяці року t	Обсяги переробки вантажів уt , тис.т.
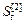
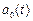
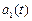
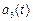
	10,3	10,3	10,3	10,3	–	–	–	–	–
	14,3	10,92	10,39	10,31	11,88	0,26	0,01	12,15	4,63
	7,7	10,42	10,40	10,33	10,39	-0,01	0,00	10,38	7,17
	15,8	11,25	10,53	10,36	12,52	0,34	0,02	12,87	8,61
	14,4	11,73	10,72	10,41	13,47	0,46	0,02	13,94	0,21
	16,7	12,50	10,99	10,50	15,03	0,66	0,03	15,71	0,98
	15,3	12,93	11,29	10,62	15,55	0,67	0,03	16,23	0,87
	20,2	14,05	11,71	10,79	17,80	0,96	0,05	18,79	2,00
	17,1	14,52	12,15	11,00	18,12	0,90	0,04	19,04	3,76
	7,5	13,44	12,35	11,21	14,49	0,18	0,00	14,67	51,39
	15,5	13,76	12,56	11,42	15,00	0,24	0,00	15,23	0,07
	16,5	14,18	12,81	11,63	15,73	0,32	0,01	16,06	0,20
(τ = 1)	16,06	14,47	13,07	11,85	16,06	0,33	0,01	16,39	–
(τ = 2)	16,39	14,76	13,33	12,08	16,39	0,33	0,01	16,72	–
(τ = 3)	16,72	15,07	13,60	12,31	16,72	0,34	0,01	17,06	–
									79,9

6. Для періоду t = 13 (t = 1) приймаємо . Далі розраховуємо , , 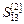, 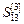коефіцієнти а ₀(13), а ₁(13) та а ₂(13), прогнозне значення . Аналогічним чином діємо для рівнів t = 14 та t = 15.

7. Розраховуємо стандартну похибку часового ряду

;

8. Розраховуємо похибку прогнозу

.

За результатами розрахунків будуємо графіки вихідного динамічного ряду та згладжених для лінійної та квадратичної функції прогнозу за методом експоненціального згладжування (рисунок 1.2).

Рисунок 1.2 – Згладжування часового ряду за методом експоненціального згладжування

Контрольні запитання

1. Дайте визначення наступним визначенням: прогноз, динамічний ряд, рівень динамічного ряду, період упередження.

2. Які види прогнозів розрізняють за тривалістю періоду упередження?

3. У чому полягає сутність методу ковзної середньої?

4. Викладіть порядок розрахунків прогнозу методом експоненціального згладжування за лінійною та квадратичною моделями. З яких міркувань обирають константу згладжування?

5. Яким чином оцінюють похибку та якість вироблених прогнозів?

Дата добавления: 2015-07-20