Построение регуляторов для объектов с полной информацией

Построение регулятора для постоянного задающего воздействия.

Рассматривается задача стабилизации ОУ при постоянном задающем воздействии

Стабилизация обеспечивается пропорциональным регулятором: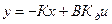

где 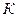- коэффициенты обратной связи. 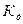-коэффициент передачи.

По заданным показателям качества, используя метод стандартных переходных функций, выберем подходящий характеристический полином замкнутой системы.

Для σ= 0 % и с учетом порядка ОУ n=2,биноминальный полином имеет вид

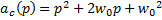
Для 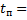0.5 с: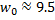

Характеристический полином замкнутой системы:

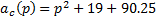
Эталонная модель:

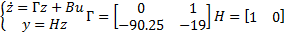
Решим матричное уравнение Сильвестра относительно матрицы М и нахйдем матрицу обратных связей .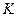

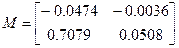
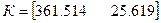
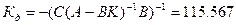- коэффициент прямой связи, позволяет добиться нулевой установившейся ошибки.

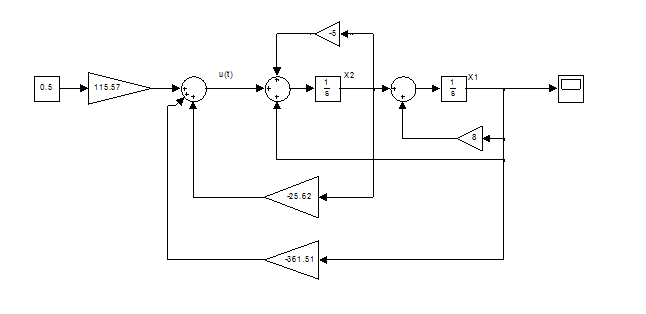
Рисунок 3.1– Модель СУ с регулятором для постоянного задающего воздействия .

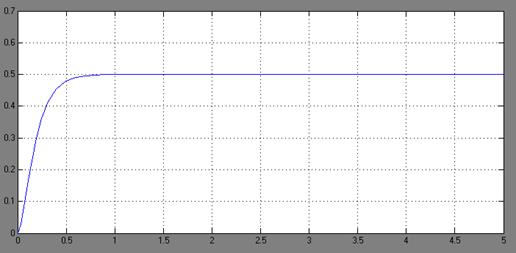
Рисунок 3.2– Результат моделированияСУ с регулятором для постоянного задающего воздействия .

Построение регулятора для линейнонарастающего задающего воздействия.

Задача слежения сводится к задаче стабилизации нулевого значения ошибки слежения.

Для сведения ошибки слежения к нулю построим комбинированный регуляторвида:

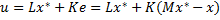
Для нахождения матриц LиMнеобходимо решить систему:

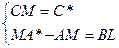
Модель линейно возрастающего задающего воздействия в форме ВСВ:

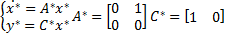
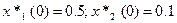
Найдем матрицы L и M:

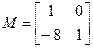
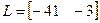
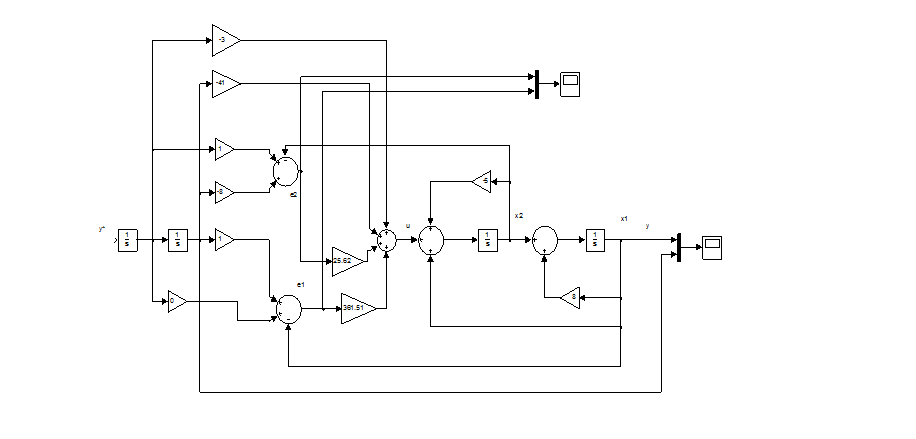
Рисунок 3.3– Модель СУ с комбинированным регулятором для линейно возрастающего задающего воздействия

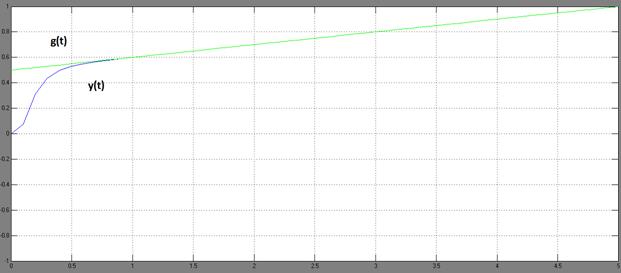
Рисунок 3.4–Результат моделирования СУ с комбинированным регулятором для линейно возрастающего задающего воздействия

Рисунок 3.5–Вектор ошибки слежения СУ с комбинированным регулятором.

t_п=0.5с –время переходного процесса

σ=0% - перерегулирование.

Построение регулятора для квадратично-нарастающего сигнала

Модель воздействия в форме ВСВ:

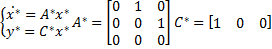
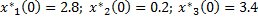
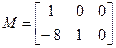
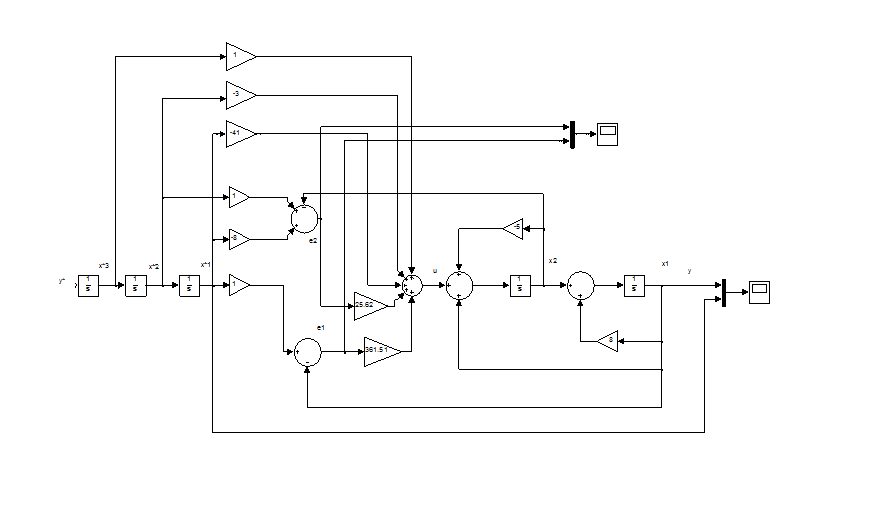
Рисунок 3.6– Модель СУ с комбинированным регулятором для квадратично-нарастающего задающего воздействия

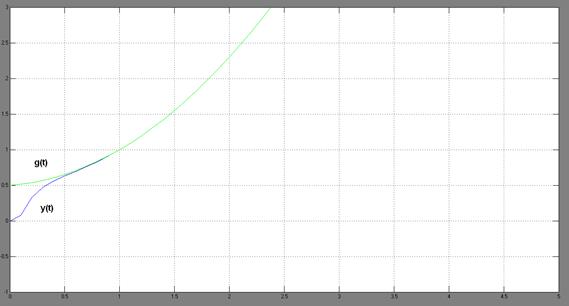
Рисунок 3.7–Результат моделирования СУ с комбинированным регулятором для квадратично-нарастающего задающего воздействия

Рисунок 3.8–Вектор ошибки слежения СУ с комбинированным регулятором.

t_п=0.5с –время переходного процесса

σ=0% - перерегулирование.

Построение регулятора длягармонического воздействия:

Модель воздействия в форме ВСВ:

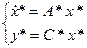
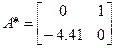
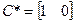
Начальные условия: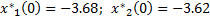

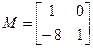
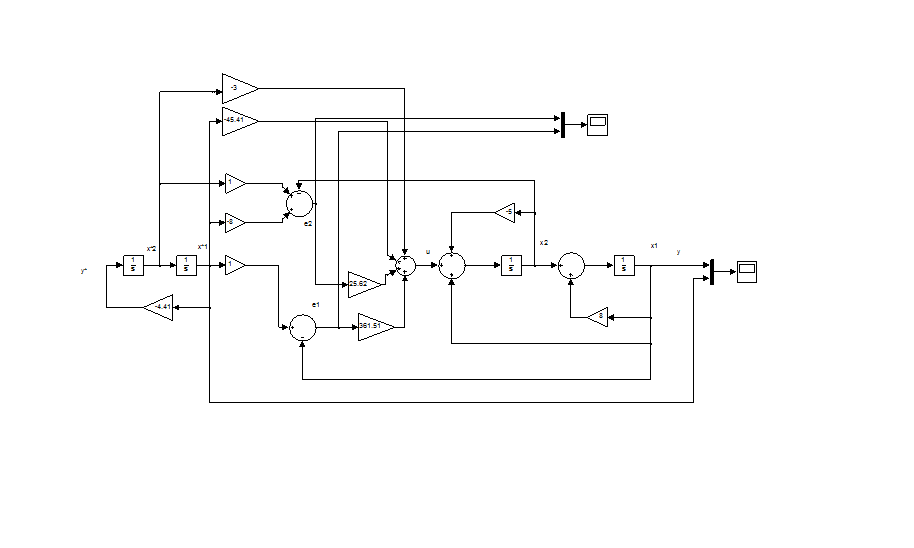
Рисунок 3.9– Модель СУ с комбинированным регулятором для гармонического воздействия:

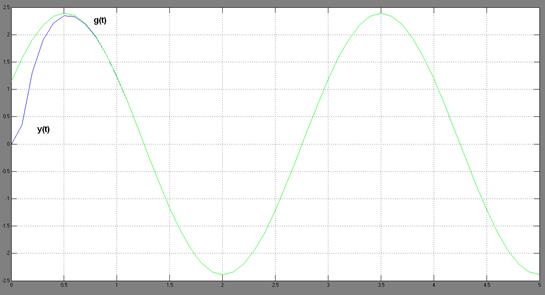
Рисунок 3.10–Результат моделирования СУ с комбинированным регулятором для гармонического воздействия:

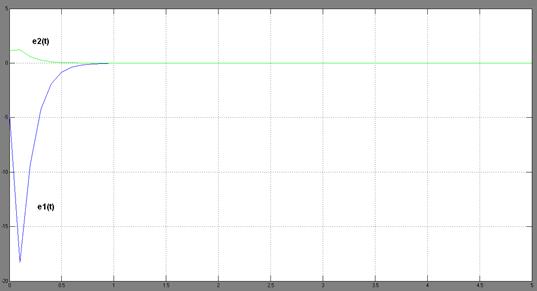
Рисунок 3.11–Вектор ошибки слежения СУ с комбинированным регулятором.

t_п=0.5с –время переходного процесса

σ=0% - перерегулирование.

Дата добавления: 2015-07-20