Зразок виконання задачі 3

Для паралельного розташування ділянок (внутрішній – прямокутна, кругла; зовнішній – трубчаста) розкрити статичну невизначуваність, з умови міцності визначити допустиме значення параметру .

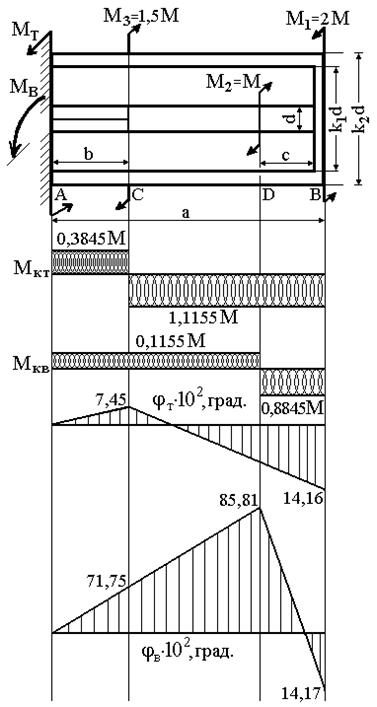Рис. 39
Геометричні характеристики перерізів: – внутрішній вал: 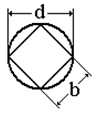квадратна частина:

кругла частина:

;

;

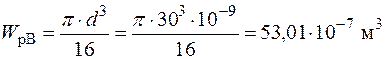зовнішня трубка:

;

.

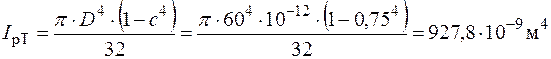2. Розкриття статичної невизначуваності:

Складаємо рівняння статики: ;

, (3.7)

М _В - опорний момент, діючий на валу;

М _Т - опорний момент, діючий на трубці в перерізі А.

Складаємо умови сумісності переміщень: кут закручування в перерізі В на валу і трубці дорівнюють одне одному:

. (3.8)

Використовуємо закон Гука для кутів закручування:

в трубці:

; (3.9)

для вала:

. (3.10)

Далі прирівнюємо отримані рівняння:

.

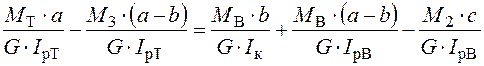Після відповідних перетворювань отримаємо:

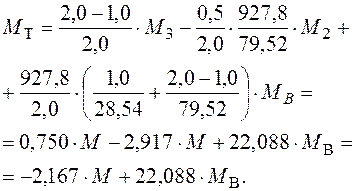(3.11)

З урахуванням рівняння (3.7), знаходимо:

Далі будуємо епюри крутних моментів в трубці і в валі.

Визначимо допустиме значення параметру з умови міцності на окремих ділянках конструкції:

для трубки:

для квадратної частини вала:

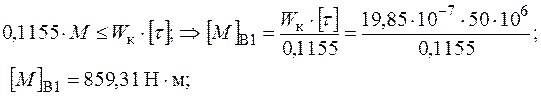
для круглої частини вала:

Таким чином, допустиме значення параметра крутного моменту визначеного з умови міцності необхідно обрати:

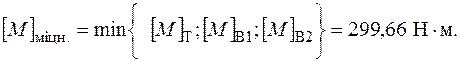
Визначимо допустиме значення параметру з умови жорсткості на окремих ділянках конструкції:

;

для трубки: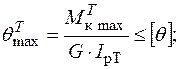

для квадратної частини вала:

для круглої частини вала:

Таким чином, допустиме значення параметра крутного моменту визначеного з умови жорсткості необхідно обрати:

Для того, щоб конструкція задовольняла умові міцності та умові жорсткості одночасно, з двох визначених допустимих значень параметра крутного моменту необхідно обрати менший.

Обчислимо абсолютні кути закручування на окремих ділянках та побудуємо епюри розподілу кутів закручування в трубці і валу:

трубка:

вал:

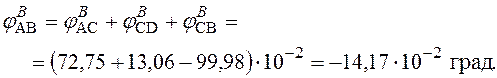
Як бачимо, кути закручування трубки і вала в перерізі В відносно нерухомого пере­різу А практично збігаються – похибка незбігу дорівнює:

Максимальний відносний кут закручування буде на ділянці DB валу:

Допустимі значення крутних моментів, визначених з умови міцності менші обраного з умови жорсткості значення, тому можна вважати, що і умова міцності буде виконуватись на всіх ділянках.

Дата добавления: 2015-07-20