|
Читайте также: |
Наближений розрахунок кручення таких тонкостінних стержнів заснований на гіпотезі Бредта про те, що дотичні напруження в поперечному перерізі розподіляються по товщині стінки рівномірно і спрямовані паралельно дотичної до серединної лінії контуру (рис. 27б). Дотичні напруження в будь-якій точці замкнутого профілю довільної форми з перемінною товщиною стінок визначаються за формулою Бредта:
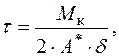(2.30)
де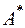 
– площа, обмежена серединною лінією профілю (рис. 27б).
Найбільше напруження виникає в тому місці контуру, де товщина стінки профілю перерізу є найменшою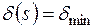 
. Умова міцності в цьому випадку запишеться у вигляді:
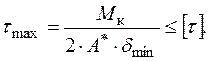(2.31)
Абсолютний кут закручування стержня довжиною 
визначається за формулою:
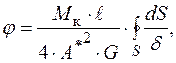(2.32)
де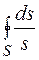 
– контурний інтеграл береться по довжині S серединної лінії контуру профілю. Якщо товщина профілю постійна 
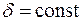, то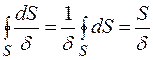 
, де S – довжина контуру серединної лінії, то формула для повного кута закручування прийме вигляд:
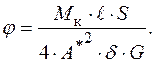(2.33)
Дата добавления: 2015-07-20; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Кручення тонкостінних стержнів | | | Кручення стержнів відкритого профілю |