Розподіл дотичних напружень при крученні стержня круглого (кільцевого перерізу). Розрахунок на міцність

З рівняння (2.10) випливає, що дотичні напруження по радіусу перерізу розподіляються лінійно (рис. 19).

Як видно з приведених на рис.19 епюр дотичних напружень, максимальні дотичні напруження виникають у крайніх точках перерізу, де :

(2.12)

Рис. 19

З огляду на те, що величина є полярним моментом опору перерізу, умова міцності при крученні запишеться у вигляді:

(2.13)

де 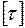– допустиме дотичне напруження, обумовлене відношенням границі текучості матеріалу до коефіцієнту запасу міцності , тобто: .

З умови міцності полярний момент опору повинний бути обраний за формулою: .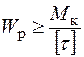

Значення полярного моменту опору для вала круглого перерізу:

.

Значення полярного моменту опору для вала кільцевого перерізу:

.

Діаметр перерізу для круглого вала обчислюється за формулою:

для кільцевого вала:

2.4 Розрахунок на жорсткість

Крім розрахунку на міцність вали розраховуються на жорсткість:

(2.14)

У деяких випадках умова жорсткості при крученні складається в абсолютних кутах закручування ( в радіанах – допустимий абсолютний кут закручування):

. (2.15)

З формули (2.14) полярний момент інерції 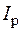, що забезпечує жорсткість, визначається як:

Полярний момент інерції:

для круглого перерізу

,

для кільцевого

.

З умови жорсткості діаметр круглого перерізу:

зовнішній діаметр кільцевого перерізу:

.

Приклад 4

Рис. 20

З умов міцності та жорсткості визначити діаметр круглого суцільного вала (рис. 20) при таких значеннях моментів, які передаються шківами: ; ; ; .

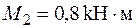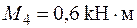Допустиме напруження , допустимий відносний кут закручування , або .

Модуль пружності сталі при зсуві .

Будуючи епюру крутних моментів, визначаємо, що найбільший момент діє на відрізку 2-3: .

Доберемо діаметр вала з умови міцності:

.

Тепер доберемо діаметр вала з умови жорсткості:

.

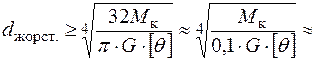
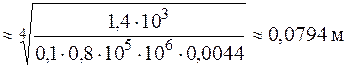Із двох діаметрів слід вибрати більший, знайдений з умови жорсткості та округлити його в більшу сторону до найближчого стандартного. Стандартний діаметр повинен мати останню цифру 0,2,5,8, якщо діаметр обирається в міліметрах. Тому значення діаметру для вала обираємо:

При цьому максимальні дотичні напруження будуть на другій ділянці валу:

.

2.5 Потенційна енергія деформації при крученні

Потенційна енергія деформації , накопичена в пружному тілі, чисельно дорівнює роботі зовнішніх сил, виконаної в процесі деформування пружного тіла. Розглянемо стержень довжиною навантажений крутним моментом (рис. 21).

Рис. 21

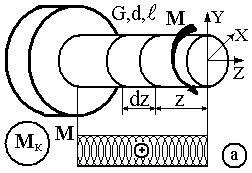
Виріжмо елементарний відрізок 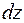і розглянемо його деформацію. Умовно закріпимо лівий переріз нескінченно малого елемента вала 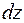. При статичному навантаженні моментом правий переріз елемента повернеться на кут (рис. 21б). Елементарна робота моменту на куті закручування при навантаженні визначається площею трикутника (рис. 21в), тобто . Кут закручування визначається за формулою (2.11) і складе: . Підставивши значення у вираз для роботи , одержимо 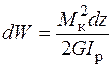, де 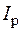– полярний момент інерції при крученні. Але робота чисельно дорівнює потенційної енергії деформації , тобто 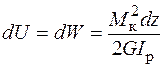. Повна потенційна енергія деформації визначається як інтеграл по довжині стержня:

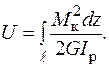(2.16)

Якщо стержень складається з декількох ділянок, потенційна енергія деформації обчислюється як сума інтегралів по ділянках:

(2.17)

2.6 Розрахунок гвинтової циліндричної пружини з малим кроком

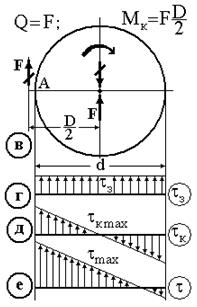
Розглянемо пружину (рис. 22а) під дією зовнішнього навантаження . Основні параметри (рис. 22б): – внутрішній діаметр пружини (діаметр утворюючої циліндра, діаметр оправки); – середній (розрахунковий) діаметр; 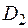– зовнішній діаметр; – діаметр прутка; – кут нахилу витка.

Рис. 22

Приведемо зовнішню силу до центра ваги поперечного переріза витка. Зневажаючи через малість поздовжньою силою і згинальним моментом , одержимо (рис. 22в) поперечну силу і крутний момент . Від дії поперечної сили (деформація зсуву, зрізу) у перерізі виникають дотичні напруження , що умовно приймемо рівномірно розподіленими по перерізу (рис. 22г) і рівними: . Від дії крутного моменту також виникають дотичні напруження, що лінійно розподіляються по перерізу (рис. 22д) і мають максимальне значення у крайніх точках перерізу:

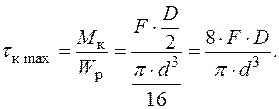
З епюр, приведених на рис. 22г та рис. 22д видно, що дотичні напруження і в т. А збігаються по напрямку.

Підсумуємо дві епюри (рис. 22г і рис. 22д) і одержимо, що в пружині найбільш навантажені внутрішні точки (точка А), а максимальні напруження:

(2.18)

де – індекс пружини. При розрахунку пружин великого діаметра D з тонкого дроту () максимальні напруження з достатнім ступенем точності можна визначити за формулою: З урахуванням напружень від поздовжньої сили, згинального моменту та поперечної сили остання формула прийме вигляд:

(2.19)

де поправочний коефіцієнт , значення якого в залежності від індексу пружини наведено нижче:

Таблиця 1

Поправочні коефіцієнти.

m
k	1,58	1,4	1,31	1,25	1,21	1,18	1,16	1,14

При визначенні осадки (деформації) гвинтової циліндричної пружини врахуємо лише деформацію від кручення. Деформаціями зсуву, розтягання – стискання та згинання зневажають через їхню малість.

Потенційна енергія деформації пружини при статичному навантаженні чисельно дорівнює роботі зовнішньої сили на відповідному переміщенні , тобто:

(2.20)

Обчислимо потенційну енергію деформації при крученні витків пружини, для чого виріжмо нескінченно малий елемент довжиною 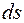(рис. 23). Жорстко закріпимо один його кінець, на вільному кінці стержня прикладемо виникаючий крутний момент .

Рис. 23

Вільний крайній переріз елементарного стержня повернеться на кут а точка прикладення сили одержить переміщення . Вважаючи незначним вплив кривизни елементарного стержня, величину потенційної енергії при крученні одного витка пружини стержня обчислимо за формулою (2.17) – .

З огляду на те, що крутний момент , полярний момент інерції , пружина має витків, потенційна енергія при статичному навантаженні пружини силою дорівнює:

. (2.21)

Порівнюючи значення потенційної енергії, що обчислюється за формулою (2.20) і (2.21), залежність для визначення осадки прийме вигляд:

(2.22)

Щоб пружина була більш податливою, діаметр прутка повинний бути найменшим, при цьому максимальні дотичні напруження досягають значних величин. Для виключення цієї невідповідності пружини виготовляються зі спеціальних пружинних матеріалів, що мають високі міцні характеристики. Приведемо значення допустимих дотичних напружень для пружинних матеріалів – високо загартовані пружинні сталі: при діаметрі прутка ; при ; при ; хромонікелеві сталі: при ; фосфористі бронзи: при .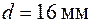

Приклад 5

Гвинтова пружина (рис. 22аб) виготовлена з дроту . Внутрішній діаметр пружини . У напруженому стані зазор на просвіт між витками . Визначити, яка потрібна сила для стискання пружини, щоб зазору не було.

Середній діаметр пружини – .

Зазор закривається, якщо осадка пружини одного витка буде дорівнювати йому, тобто:

,

звідки: .

Приклад 6

Рис. 24

Для двох циліндричних гвинтових пружин, осі яких співпадають (рис.24), навантажених силою , визначити напруження. Середні діаметри пружин: Діаметри прутків: Число витків: Матеріал двох пружин однаковий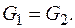

Для розрахунку на міцність, необхідно визначити зусилля, що діють на кожну пружину окремо.

Позначимо через та 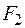зусилля, що діють у відповідних пружинах.

Застосувавши рівняння рівноваги маємо:

.

В даному випадку пружини мають однакову осадку, тобто переміщення вздовж їхньої осі однакові – 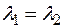. Згідно з (2.22):

Враховуючи чисельні дані отримаємо:

Використовуючи рівняння рівноваги, знайдемо:

Згідно (2.19) з урахуванням того, що поправочні коефіцієнти 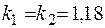для (див. табл. 1), дотичні напруження в першій пружині будуть дорівнювати:

а в другій –

Для високо загартованої пружинної сталі та даних діаметрів прутків . Таким чином, умова міцності для обох пружин виконується.

Приклад 7

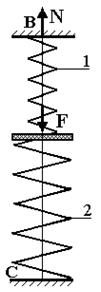Рис. 25

Для двох циліндричних, послідовно розташованих гвинтових пружин, осі яких співпадають (рис. 25), навантажених через абсолютно жорсткий диск силою , визначити напруження. Середні діаметри пружин: Діаметри прутків: Число витків:

Матеріал двох пружин однаковий

Для розрахунку на міцність, необхідно визначити зусилля, що діють на кожну пружину окремо.

Позначимо через та 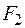зусилля, що діють у відповідних пружинах. При цьому ; .

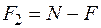В даному випадку осадка пружин, тобто переміщення вздовж їхньої осі буде дорівнювати – . Згідно з (2.22):

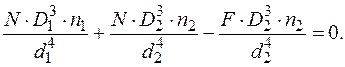
Враховуючи чисельні дані отримаємо значення зусиль в пружинах:

При цьому перша пружина працює на розтягання, а друга на стискання.

Згідно (2.19) з урахуванням того, що поправочні коефіцієнти 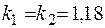для (див. табл. 1), дотичні напруження в першій пружині будуть дорівнювати:

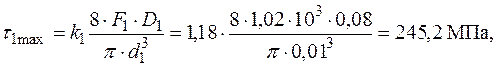
а в другій –

Для високо загартованої пружинної сталі та даних діаметрів прутків . Таким чином, умова міцності для обох пружин виконується.

Дата добавления: 2015-07-20