Кручення стержнів відкритого профілю

При розрахунку стержнів відкритого профілю варто розрізняти прості і складені перерізи. Приклади простих профілів (перерізів) приведені на рис. 28.

Рис. 28

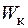Ці профілі характеризуються тим, що можуть бути розгорнуті у витягнутий прямокутник висотою S і шириною d. Для вузького прямокутного перерізу (рис. 29), коли , коефіцієнти і моменти опору та інерції запишуться як , і формули (2.23–2.25) для визначення максимальних дотичних напружень , відносного 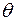і абсолютного кутів закручування запишуться у вигляді:

; ; .

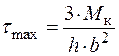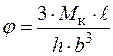Епюра розподілу дотичних напружень представлена на рис. 29. По всій довжині профілю 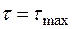, по ширині поперечного перерізу дотичні напруження змінюються за лінійним законом.

Рис. 29

Приведеними формулами можна користатися і для тонкостінних незамкнутих профілів з криволінійним контуром постійної товщини , якщо замість підставити довжину серединної лінії перерізу, а замість 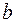– товщину профілю (рис. 28).

Для складених стержнів відкритого профілю, що складаються з декількох вузьких прямокутників різної товщини (типу швелер, кутник, двотавр) величину моменту інерції при крученні можна визначити за формулою:

, (2.34)

де коефіцієнт 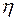залежить від форми перерізу (для куткового – ; двотаврового – ; таврового – ; швелерного – ).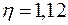

Момент опору при крученні запишеться як:

,

а максимальні дотичні напруження визначаться як:

. (2.35)

Найбільші напруження в кожному елементі визначаються за формулою:

.

Абсолютний кут закручування j визначається як:

. (2.36)

Приклад 8

Зіставити величини найбільших дотичних напружень і кутів закручування для сталевих стержнів довжиною , діаметром , товщиною стінки мм для випадків відкритого (рис. 30а) і закритого (рис. 30б) профілів, навантажених однаковими крутними моментами .

Рис. 30

Стержень відкритого профілю (рис. 30а).

Розгорнемо профіль у витягнутий прямокутник зі сторонами:

,

.

Максимальні дотичні напруження обчислимо за формулою:

.

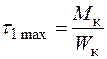Момент опору на кручення:

.

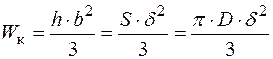Тоді максимальні дотичні напруження виявляються рівними:

.

Абсолютний кут закручування обчислимо за формулою:

.

Момент інерції на кручення:

.

У цьому випадку кут закручування дорівнює:

.

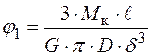Стержень закритого профілю (рис. 30б).

Максимальні дотичні напруження обчислимо за формулою Бредта:

,

де , і одержимо:

.

Кут закручування обчислимо за формулою:

.

Після перетворень одержимо:

.

Відношення напружень:

.

Відношення кутів закручування:

.

Отже, стержень замкнутого профілю виявляється істотно більш міцним та в ще більшому ступені жорстким, чим такий же незамкнутий.

Дата добавления: 2015-07-20