
|
Читайте также: |
2) Находим  .
.
3) Сравнивая значения во внутренней критической точке  и на концах
и на концах 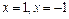 , заключаем: наибольшее значение
, заключаем: наибольшее значение  на отрезке
на отрезке  равно 5, т.е.
равно 5, т.е.  , а наименьшее значение
, а наименьшее значение  на этом отрезке равно нулю (в точке
на этом отрезке равно нулю (в точке  ).
).
б) На участке АВ имеем  где
где 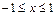 :
:
Ищем наибольшее и наименьшее значения  на отрезке
на отрезке  :
:
1)  внутри данного отрезка
внутри данного отрезка  при
при  ;
;  .
.
2) Находим 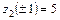 .
.
3) Наибольшее значение  на отрезке
на отрезке  равно 5 в точках
равно 5 в точках  , а наименьшее значение
, а наименьшее значение 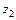 на этом отрезке равно 0,77 (в точке
на этом отрезке равно 0,77 (в точке  ).
).
Сопоставляя значения 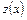 на участках АОВ и АВ, приходим к выводу: на всей границе наибольшее значение функции
на участках АОВ и АВ, приходим к выводу: на всей границе наибольшее значение функции  равно 5 (в точках А и В, а ее наименьшее значение равно 0 (в точке О).
равно 5 (в точках А и В, а ее наименьшее значение равно 0 (в точке О).
III. Внутри заданной замкнутой области  функция
функция  не имеет точек экстремума, ее наибольшее и наименьшее значения достигаются в точках, лежащих на границе этой области. В граничных точках
не имеет точек экстремума, ее наибольшее и наименьшее значения достигаются в точках, лежащих на границе этой области. В граничных точках  и
и 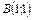 функция
функция  имеет наибольшее значение,
имеет наибольшее значение, 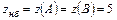 , а в граничной точке
, а в граничной точке  она имеет наименьшее значение,
она имеет наименьшее значение, 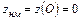 .
.
Задача № 17. Найти неопределенные интегралы, ответ проверить дифференцированием.
 ,
,  ,
, 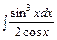 .
.
Решение:
 .
.
Проверка:  (верно).
(верно).

 .
.
Проверка: 
 (верно).
(верно).
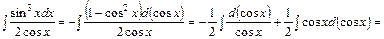
 .
.
Проверка: 
 (верно).
(верно).
Задача № 18. Вычислить длину дуги кривой  (Спираль Архимеда).
(Спираль Архимеда).
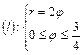
Решение: Воспользуемся формулой (55):



 .
.
Т.е. получили 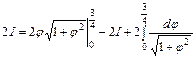 .
.
Далее, перенося искомый интеграл  из правой части равенства в левую и заменяя интеграл, оставшийся в правой части равенства, по формуле 10 из таблицы интегралов, получим
из правой части равенства в левую и заменяя интеграл, оставшийся в правой части равенства, по формуле 10 из таблицы интегралов, получим

Таким образом, 
Имеем 
Ответ:  .
.
Глава V. Задачи для контрольных заданий
1. Определители и матрицы. Системы линейных уравнений
Задача № 1
Вычислить определители 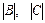 :
:
1.1 
1.2 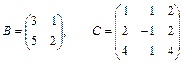
1.3 
1.4 
1.5 
1.6 
1.7 
1.8 
1.9 
1.10 
1.11 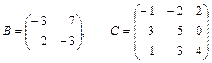
1.12 
1.13 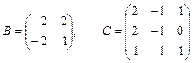
1.14 
1.15 
1.16 
1.17 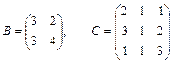
1.18 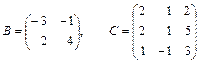
1.19 
1.20 
1.21 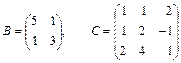
1.22 
1.23 
1.24 
1.25 
1.26 
1.27 
1.28 
1.29 
1.30 
Задача № 2
Решить систему  двумя способами:
двумя способами:
а) методом Гаусса;
б) по формулам Крамера, где  – матрица из задачи 1,
– матрица из задачи 1, 
2.1 
| 2.2 
|
2.3 
| 2.4 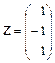
|
2.5 
| 2.6 
|
2.7 
| 2.8 
|
2.9 
| 2.10 
|
2.11 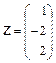
| 2.12 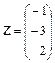
|
2.13 
| 2.14 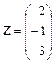
|
2.15 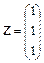
| 2.16 
|
2.17 
| 2.18 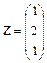
|
2.19 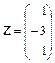
| 2.20 
|
2.21 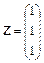
| 2.22 
|
2.23 
| 2.24 
|
2.25 
| 2.26 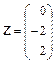
|
2.27 
| 2.28 
|
2.29 
| 2.30 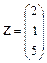
|
2. Векторная алгебра
Задача № 3
Варианты 3.1 – 3.4: Найти угол между векторами  и
и 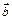 .
.
Варианты 3.5 – 3.10: Вычислить площадь параллелограмма, построенного на векторах  и
и 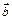 .
.
Варианты 3.11 – 3.18: Вычислить проекцию одного вектора на другой.
Варианты 3.19 – 3.24: Вычислить величину момента силы  , приложенной к точке А относительно точки О, если
, приложенной к точке А относительно точки О, если  .
.
Варианты 3.25 – 3.30: Вычислить работу силы  , если ее точка приложения, двигаясь прямолинейно, вращается вдоль вектора
, если ее точка приложения, двигаясь прямолинейно, вращается вдоль вектора  .
.
3.1 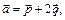



3.2 



3.3 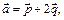

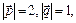

3.4 
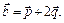
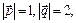

3.5 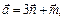


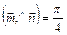
3.6 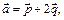

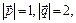

3.7 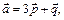

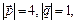

3.8 
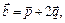

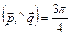
3.9 


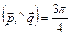
3.10 



3.11 


Найти 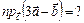
3.12 

Найти 
3.13 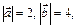
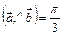
Найти 
3.14 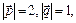

Найти 
3.15 

Найти 
3.16 
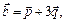


Найти 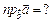
3.17 

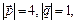
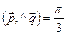
Найти 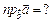
3.18 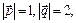



Найти 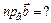
3.19 
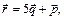
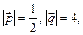
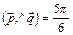
3.20 


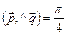
3.21 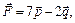



3.22 



3.23 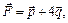


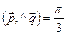
3.24 
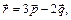
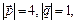
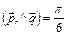
3.25 



3.26 



3.27 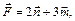



3.28 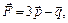


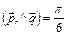
3.29 



3.30 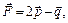


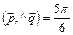
Задача № 4
Даны координаты вершин пирамиды 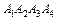 . Найти:
. Найти:
а) площадь грани 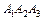 ,
,
б) объем пирамиды.
4.1 
4.2 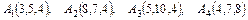
4.3 
4.4 
4.5 
4.6 
4.7 
4.8 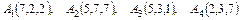
4.9 
4.10 
4.11 
4.12 
4.13 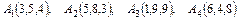
4.14 
4.15 
4.16 
4.17 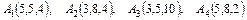
4.18 
4.19 
4.20 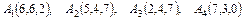
4.21 
4.22 
4.23 
4.24 
4.25 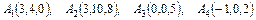
4.26 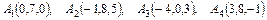
4.27 
4.28 
4.29 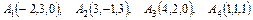
4.30 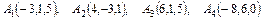
3. Аналитическая геометрия на плоскости
Задача № 5
Дано уравнение прямой. Записать его в следующих видах:
1. Уравнение в отрезках.
2. Уравнение с угловым коэффициентом
Построить прямую в системе координат.
| 5.1 | 
| 5.2 | 
|
| 5.3 | 
| 5.4 | 
|
| 5.5 | 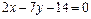
| 5.6 | 
|
| 5.7 | 
| 5.8 | 
|
| 5.9 | 
| 5.10 | 
|
| 5.11 | 
| 5.12 | 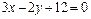
|
| 5.13 | 
| 5.14 | 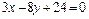
|
| 5.15 | 
| 5.16 | 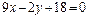
|
| 5.17 | 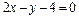
| 5.18 | 
|
| 5.19 | 
| 5.20 | 
|
| 5.21 | 
| 5.22 | 
|
| 5.23 | 
| 5.24 | 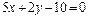
|
| 5.25 | 
| 5.26 | 
|
| 5.27 | 
| 5.28 | 
|
| 5.29 | 
| 5.30 | 
|
Дата добавления: 2015-07-20; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замечание. 3 страница | | | Замечание. 5 страница |