Определение. Матрицу , получаемую из матрицы А заменой строк и столбцов друг на друга, называют транспонированной.

Например, если , то .

1. Любую матрицу можно умножить на любое действительное число : .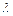

2. Матрицы одной и той же размерности можно складывать (вычитать):

3. Матрицу А можно умножать на матрицу В только, если число столбцов матрицы А равно числу строк матрицы В:

,

причем элементы матрицы С находятся по правилу:

,

то есть элементы i– ой строки матрицы А умножаются на соответствующие элементы j –го столбца матрицы В и полученные произведения складываются.

§ 2. Определители и их вычисление.

Каждой квадратной матрице по определенному правилу ставится в соответствие число, называемое определителем.

1. Правило вычисления определителя 2-го порядка:

2. Правило вычисления определителя 3-го порядка – правило треугольников:

Правило разложения определителя по элементам 1-й строки:

, где алгебраические дополнения , а минор – определитель, получающийся из данного путем вычеркивания i- ой строки и j- го столбца.

Таким образом,

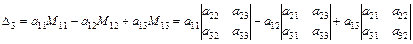
Аналогично определитель можно раскладывать по элементам любой строки или столбца.

3. Правило вычисления определителя n –го порядка. Определители n –го порядка вычисляются также разложением по элементам любой строки или столбца.

Таким образом,

– разложение определителя по элементам i –ой строки

или

– разложение определителя по элементам j –го столбца

§ 3. Решение систем линейных уравнений

1. Формулы Крамера для решения систем трех линейных уравнений с тремя неизвестными:

где

2. Метод Гаусса.

Сущность метода состоит в том, что посредством последовательных исключений неизвестных, данная система преобразуется в систему ей эквивалентную. Последовательное исключение неизвестных осуществляется с помощью элементарных преобразований системы:

а) перестановок двух любых уравнений;

б) умножений обеих частей одного из уравнений на любое, отличное от нуля число;

в) прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.

Заметим, что удобно работать не с самими уравнениями системы, а с ее расширенной матрицей.

Дата добавления: 2015-07-20