Пример. Переставим местами два первых уравнения

Переставим местами два первых уравнения

Составим расширенную матрицу системы

Первую строку умножим на «–2» и сложим со второй строкой.

Первую строку умножим на «–1» и сложим с третьей строкой.

Получаем матрицу:

Вторую строку умножим на «–1» и сложим с третьей:

Этой матрице соответствует система уравнений:

Глава II. Элементы векторной алгебры и аналитической геометрии

§ 1. Векторы. Основные понятия

Вектор – направленный отрезок (рис.1).

Рис. 1 Если точка – начало вектора, точка – конец вектора, то координаты вектора .

Вектор записывают также через единичные Рис. 1

векторы осей : (на плоскости) (рис. 2), (в пространстве).

Пусть , тогда

. (1)

Расстояние между точками и :

(2)

(2')

Координаты точки С, являющейся серединой отрезка АВ:

(3)

Длина вектора : (4)

(4')

§ 2. Скалярное произведение векторов

Определение. . (5)

Если , то

(6)

Из формулы (5) имеем угол между векторами и :

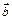(7)

Проекция вектора на вектор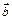

Физический смысл скалярного произведения

Пусть материальная точка движется по прямой от точки до точки , проходя при этом путь .

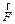Допустим, что на точку действует сила , постоянная по величине и направлению и составляющая с направлением перемещения точки угол .

Из физики известно, что работа , совершаемая при этом силой 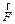на участке равна , где , или .

Свойства:

1) ,

2) ,

3) если , то

Замечание:

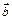
а) || или .

б) или .

§ 3. Векторное произведение векторов

Определение. – вектор, удовлетворяющий трем условиям:

1) ,

2) ,

3) образуют правую тройку, то есть, если смотреть из конца , то кратчайший поворот от к 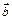виден против часовой стрелки (рис. 3).

Замечание: Если вектор изображает силу, приложенную к точке А, а вектор направлен из некоторой точки О в точку А, то вектор представляет собой момент силы относительно точки О: (8)

Свойства:

1) ,

2) , если , либо , либо || ,

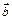3) ,

4) .

Если известны координаты векторов, то

(9)

Площадь параллелограмма, построенного на векторах и :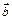

– площадь треугольника (10)

§ 4. Смешанное произведение векторов

Смешанным произведением векторов называют число, равное . Обозначают также .

Если известны координаты векторов, то

Объем пирамиды равен (11)

Дата добавления: 2015-07-20