Канонічне рівняння прямої

Тема. ЛІНІЇ НА ПЛОЩИНІ. | Рівняння прямої,що проходить через дану точку перпендикулярно до даного вектора | Загальне рівняння прямої |

Читайте также:

Дохідний підхід за методом прямої капіталізації.
Загальне рівняння прямої
Загальні відомості про об’єкти порівняння
Задача 1. Скласти рівняння гіперболи з фокусами на осі Ох, якщо довжина її уявної осі дорівнює 12, і гіпербола проходить через точку (20;8).
Задача 10.Скласти рівняння площини, яка проходить через пряму і точку М(1;-3;5).
Задача 2.Складіть рівняння кола, яке має центр в точці (5;-7) і проходить через точку (2;-3).
Задача 4. Скласти рівняння гіперболи з фокусами на осі Ох, якщо довжина її дійсної осі дорівнює 16, і гіпербола проходить через точку (-10;-3).

Нехай пряма проходить через задану точку M0(x0; у0) паралельно даному векторові = (l, m) (рис. 3.8).

Виберемо на прямій довільну точку М (х; у) і розглянемо вектор M0M =(х-х0,у-у0). Вектори 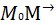і колінеарні, тому їхні координати пропорційні. З цієї умови дістанемо рівняння

(3.9)

яке називають канонічним рівнянням прямої. Вектор називають напрямним вектором прямої.

Дата добавления: 2015-07-20; просмотров: 69 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Рівняння прямої з кутовим коефіцієнтом	\|	Рівняння прямої, що проходить через дві задані точки

mybiblioteka.su - 2015-2024 год. (0.006 сек.)