Рівняння прямої, що проходить через дві задані точки

Нехай пряма проходить через дві задані точки M1(х1; y1) і М2(х2, у2) (рис. 3.9). Тоді напрямним вектором прямої буде = M1M
= (х2 - х1,y2-y1)- Підставивши його координати й координати заданої точки M1 (х1;y1) у рівняння (3.9), дістанемо рівняння

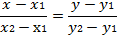(3.10)

яке називають рівнянням прямої, що проходить через дві задані

точки.

Приклад 4. Запишемо рівняння прямої, що проходить через точки M1(3; 1) і M2 (5; 4),

Підставляючи координати заданих точок у рівняння (3.10), діста­немо рівняння шуканої прямої:

або або 3x-2y-7=0

Рівняння прямої у відрізках

Запишемо рівняння прямої, яка відтинає від осей координат Ох і Oу задані відрізки α≠ 0 і Ь ≠ 0 відповідно (рис. 3.10).

Використовуючи рівняння пря­мої (3.10), яка проходить через точ­ки А{а;0) і B(0; b), дістанемо рівняння

,або після перетворень
(3,11)

Рівняння (3.11) називають рівнян­ням

прямої у відрізках. Його зруч­но використовувати під час побу­дови прямої.

Приклад 5. Запишемо рівняння прямої, що проходить через точку М (4; -1)і відтинає від додатної півосі Ох відрізок удвоє більший, ніж на додатній півосі Оу, й побудуємо цю пряму

За умовою а = 2Ь (а > 0, Ь > 0).

Підставивши ці значення в рівняння (3.11), дістанемо

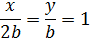
Оскільки точка М (4; -1) лежить на прямій, то її координати задовольня­ють це рівняння. Отже

Звідси b=1. Тоді а = 2. Рівняння шуканої прямої (рис. 3.11) має вигляд

Дата добавления: 2015-07-20