Рівняння прямої з кутовим коефіцієнтом

Нехай пряма перетинає вісь Oy у точці B(0; Ь) й утворює з віссю Ох кут α (рис 3.4) який називають кутом нахилу прямої

Виберемо на прямій довільну точку М(x;y).

Розглянемо трикутник MBN, в якому

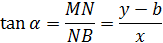
Означення:. Кутовим коефіцієнтом гіршої називають тан­генс кута а, який утворює пряма з додатним напрямом осі Ох:

k = tg α. (3.5)

Отже, K= ,звідки

у = kx + Ь. (3.6)

Рівняння (3.6) називають рівнянням прямої з кутовим коефіцієн­том.

Розглянемо окремі випадки рівняння (3.6).

Якщо Ь = 0, то пряма у = kx проходить через початок координат (рис. 3.5). Якщо k = tg α > 0,то пряма утворює з віссю Ох гострий кут. Якщо ж k=tg α < 0, то пряма утворює з віссю Ох тупий кут

2. Якщо k = 0, то tg α = 0, а отже, α = 0; тому пряма у = b паралель­на осі Ох. Рівняння осі Ох має вигляд у= 0 (рис. 3.6).

3. Якщо α = π/2, то tg(π/2) не існує, тобто вертикальна пряма не має кутового коефіцієнта. Дана пряма паралельна осі Оу, і її рівняння має вигляд х=α (рис. 3.7).

Дата добавления: 2015-07-20